Building groups: semidirect products

Now we find a homomorphism from H to aut(N). Then the elements of H permute the elements of N, according to the automorphism that they map to.

If we choose a homomorphism whose kernel is the whole of H, the method described here will work but will just build N×H. For any other homomorphism, it will build a non-Abelian group whose order is the product of the orders of N and H, which has N as a normal subgroup, and which has H as a non-normal subgroup. If the homomorphism is injective, and every (non-identity) element of its image permutes every (non-identity) element of N, the result is a Frobenius group. If the homomorphism is bijective, the result is the holomorph of N and H.

Strategy hint. In choosing a homomorphism, try to map H to outer automorphisms of N. If you choose inner homomorphisms, the method will work, but you are likely to end up with a group that you already knew, or could have built more easily by other methods. Fortunately, if N is Abelian, this is not an issue: all automorphisms of Abelian groups are outer.

Formally, if N is {n₁, n₂, .. n_a; +} and H is {h₁, h₂, .. h_b; *}, then the elements of the semidirect product are the ordered pairs (n_i, h_j) and its operation is such that (n_i, h_j)(n_k, h_l) = (n_i+n_k', h_j*h_l) where n_k' is what n_k is mapped to by the element of aut(N) that our chosen homomorphism takes h_j to.

More comprehensibly, the elements of H permute the elements of N according to the homomorphism. This should be made clearer by the following examples.

Example 1: C3⋊C2

The automorphism group of C3 is C2. There are two homomorphisms from C2 to C2; we will only consider the bijective one (the other, with the whole C2 in its kernel, just results in the direct product C3×C2).

Let us present our C3 as < a | a³ > and our C2 as < b | b² >. In our chosen homomorphism, b performs the permutation (a aa) on the C3. So whenever we have a to the right of b, it becomes aa when we move it to the left; and whenever we have aa to the right of b, it becomes a when we move it to the left. So ba=aab and baa=ab. The presentation of this C3⋊C2 is < a,b | a³=1, b²=1, ba=a²b > or, rather more obscurely, < a,b | a³, b², abab >.

Example 2: (C2×C2)⋊C3

The automorphism group of (C2×C2) is D6. D6 has C3 as a subgroup, so there are two homomorphisms from C3 to D6; we will consider only the injective one (the other just results in the direct product C2×C2×C3).

Let us present our (C2×C2) as < a,b | a², b², (ab)² > and our C3 as < t | t³ >. In our chosen homomorphism, t performs the permutation (a b ab) on the C2×C2, and t² performs (a ab b). So whenever we have a to the right of t, it becomes b when we move it to the left; whenever we have b to the right of t, it becomes ab when we move it to the left; and whenever we have ab to the right of t, it becomes a when we move it to the left. So ta=bt, tb=abt, and tab=at. The presentation of this (C2×C2)⋊C3 is < a,b,t | a²=1, b²=1, t³=1, ta=bt, tb=abt > or, rather more obscurely, < a,b,t | a², b², t³, tatb, tbtab >.

Example 3: C8⋊C2

The automorphism group of C8 is (C2×C2). (C2×C2) has C2 as a quotient group in four different ways, so there are four homomorphisms from C2 to (C2×C2). We will consider each of these.

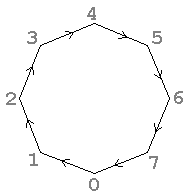
Let us regard our C8 as the integers under addition modulo 8, as shown in the Cayley graph to the right.

The four automorphisms are found by multiplying the integers by 1, by 3, by 5 and by 7. Mutiplying by 1 is the trivial automorphism.
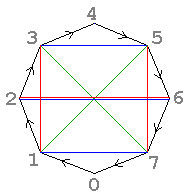another Cayley graph for C8

The three non-trivial automorphisms are shown overlaid on the C8 Cayley diagram to the right: ×3 in red, ×5 in green, and ×7 in blue. Thus the ×3 automorphism does the permutation (1 3)(5 7); ×5 does (1 5)(2 6)(3 7); and ×7 does (1 7)(2 6)(3 5).

These four automorphisms give the four distinct groups C8⋊C2 whose presentations and Cayley diagrams are shown in the table below.

Example 4: C3⋊D8

The automorphism group of C3 is C2. D8 has C2 as a quotient group in three different ways, so there are four homomorphisms from D8 to C2. We will consider each of these.

The first maps the whole D8 to the identity of the C2. As usual, if we use this homomorphism we will get the direct product C3×D8.

Let us regard the D8 as < a,b | a⁴, b², abab >. The second homomorphism maps {1,a,aa,aaa} to the identity of the C2 and {b,ab,aab,aaab} to the other element. In effect we are treating the D8 as C4⋊C2, and letting the C2 permute a C3 as well as the C4 that it is already permuting. Thus the C2 is permuting both a C4 and a C3, which do not interact with each other; so the group (known as the pullback of D8×D6 by C2) is (C3×C4)⋊C2 = C12⋊C2 = D24. This is not so interesting, there is an easier way to build D24.

The third homomorphism maps {1,aa,b,aab} to the identity of the C2 and {a,aaa,ab,aaab} to the other element. If we were in the habit of regarding D8 as C4⋊C2, we might have thought that C4 was its only normal subgroup of order 4, and overlooked this homomorphism. But if we had examined it carefully when we first built it, we would have realised that it also has C2×C2 as a normal subgroup, giving a different C2 as a quotient group within it. That is the point of this example.

A presentation of the C3⋊D8 that uses this third homomorphism is < a,b,c | a⁴, b², c³, abab, bcb^-1c^-1, cac^-1a >.

The fourth homomorphism maps {1,aa,ab,aaab} to the identity of the C2 and {a,aaa,b,aab} to the other element. The C3⋊D8 that uses this fourth homomorphism is isomorphic to that using the third.

The next four examples are related. They are C7⋊C6, C7⋊S3, (C2×C2)⋊C6 and (C2×C2)⋊S3.
We will refer to the two groups as A and B, where we are trying to build a semidirect product A×B.
We will use H to denote the "action" of B on A.
H must be a subgroup of Aut(A), and must be isomorphic to a quotient of B.
Where H is the trivial group, we just get the direct product A×B.
Where Aut(A)≅H≅B, we get what is called the holomorph of A.

Example 5: A is C7, B is C6.

Aut(A) is C6, which has four subgroups: 1, C2, C3, C6.

B has four quotient groups: 1, C2, C3, C6.

So H can be any group common to these two lists, i.e. 1, C2, C3, C6.

If we take H=1, we get the direct product of A and B. It is C7×C6, also known as C42.
If we take H=C2, the action of H extends A from C7 to D14, and the C3 part of B does not interact with A. Thus we get D14×C3.
If we take H=C3, the action of H extends A from C7 to Frob21, and the C2 part of B does not interact with A. Thus we get Frob21×C2.
If we take H=C3, the action of H extends A from C7 to Frob42. This is the holomorph of C7.

Example 6: A is C7, B is S3.

Aut(A) is C6, which has four subgroups: 1, C2, C3, C6.

B has three quotient groups: 1, C2, S3.

So H can be any group common to these two lists, i.e. 1, C2.

If we take H=1, we get the direct product of A and B. It is C7×S3.
If we take H=C2, and regard B as C3⋊C2, we see that the C2 that is acting on the C3 (to extend it to S3) is also now acting on the C7 to extend it to D14. This gives D42.

Example 7: A is C2×C2, B is C6.

Aut(A) is S3, which has four subgroups: 1, C2, C3, S3.

B has four quotient groups: 1, C2, C3, C6.

So H can be any group common to these two lists, i.e. 1, C2, C3.

If we take H=1, we get the direct product of A and B. It is C2×C2×C6, which we can also regard as C2×C2×C2×C3.
If we take H=C2, the action of H extends A from C2×C2 to D8. The C3 subgroup of B does not interact with A. So the result is D8×C3.
If we take H=C3, the action of H extends A from C2×C2 to A4. The C2 subgroup of B does not interact with A. So the result is A4×C2.

Example 8: A is C2×C2, B is S3.

Aut(A) is S3, which has four subgroups: 1, C2, C3, S3.

B has four quotient groups: 1, C3, S3.

So H can be any group common to these two lists, i.e. 1, C3, S3.

If we take H=1, we get the direct product of A and B. It is C2×C2×S3.
If we take H=C2, the action of H extends A from C2×C2 to D8. But H is the same C2 that extends C3 to the S3 that is B. So we can regard the result as a D8 (formed from A and part of B) acting on a C3 (the other part of B), and describe the result as C3⋊D8.
If we take H=S3, we get S4. This is the holomorph of C2×C2.

Summary

Now that we can build direct and semidirect products, we can, starting from cyclic groups, build 88 of the 93 groups of order less than 32

C8⋊C2, trivial automorphism = C8×C2	< k,r \| k⁸=1, r²=1, kr=kr > < k,r \| k⁸, r², krk^-1r >
C8⋊C2, blue *7 automorphism = D16	< k,r \| k⁸=1, r²=1, kr=rk⁷ > < k,r \| k⁸, r², krkr >
C8⋊C2, green *5 automorphism known as the "modular" group of order 16	< k,r \| k⁸=1, r²=1, kr=rk⁵ > < k,r \| k⁸, r², krkkkr >
C8⋊C2, red *3 automorphism known as the "quasidihedral" group of order 16	< k,r \| k⁸=1, r²=1, kr=rk³ > < k,r \| k⁸, r², krkkkkkr >

How to Build Groups: Semidirect Products

Introduction