Valid and Invalid Cayley Diagrams

This is a sub-page of How to Build Groups.
It is linked to from the page Toll-bean Extensions.

Introduction

For any group, it is possible to draw a Cayley diagram, probably in many different ways.
To every valid Cayley diagram, there corresponds a group.
Some things that superficially look like Cayley diagrams do not correspond to any group. We call such diagrams "invalid Cayley diagrams".

This page explains how to tell if a given diagram is valid.

Conditions for Validity

A Cayley diagram is a set of vertices and a set of arcs. Each arc connects two vertices, has a colour, and may have an arrow. An arrowed arc runs only in the direction of the arrow; a plain arc runs in both directions.

A Cayley diagram is valid if and only if

Every vertex has exactly one incoming arc of each colour.
Every vertex has exactly one outgoing arc of each colour.
If, starting at some vertex, following some sequence of colours takes you back to that starting vertex, then that sequence of colours takes you back to the starting vertex wherever you start.

Violations of conditions 1 and 2 are easy to detect. The examples on this page of invalid Cayley diagrams all violate condition 3.

Some Examples

In all these examples, the colours will be denoted as follows: k=black, r=red, g=green, b=blue


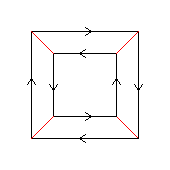
Fig. 1

This Cayley diagram is valid. Each vertex has one incoming black arc, one outgoing black arc, and one red arc which is both incoming and outgoing. For every starting vertex, any of the sequences rr, rkrk, rkkrkk, rkkkrkkk, kkkk leads back to the starting vertex.


Fig. 2

This Cayley diagram is valid. Each vertex has one incoming black arc, one outgoing black arc, and one red arc which is both incoming and outgoing. For every starting vertex, any of the sequences rr, kkk, rkrkrk, krkkrkkrk leads back to the starting vertex.


Fig. 3

This Cayley diagram is invalid. Each vertex has one red arc, one green arc, and one blue arc, each both incoming and outgoing. However from four of the vertices the sequence rgb leads back to the starting vertex, and from eight of them it does not.

This is disappointing. The diagram has plenty of pleasing symmetry.


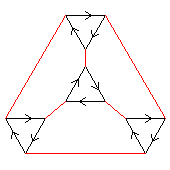
Fig. 4

This Cayley diagram is valid. Each vertex has one incoming black arc, one outgoing black arc, and one red and one green arc each both incoming and outgoing. For every starting vertex, any of the sequences rr, gg, k⁷, rkrk, gkgk, rg⁷, (rgk)⁷ leads back to the starting vertex.


Fig. 5

This Cayley diagram is invalid. Each vertex has one red arc, one green arc, and one blue arc, each both incoming and outgoing. However from four of the vertices the sequence rbrgb leads back to the starting vertex, and from sixteen of them it does not.


Fig. 6

This Cayley diagram is invalid. At some vertices, (kr)²=1, at others (kr)³=1.


Fig. 7

This Cayley diagram is invalid. Each vertex has one red arc and one black arc, each both incoming and outgoing. However from the two right vertices the sequence kk leads back to the starting vertex with no bean, while from the two left vertices it leads back to the starting vertex with one bean.

For a Cayley diagram to be valid, all order-2 (not arrowed) arcs of the same colour must have identical toll stations


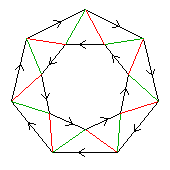
Fig. 8

This Cayley diagram is valid. Each vertex has one red arc and one black arc, each both incoming and outgoing. For every starting vertex, any of the sequences r⁴, k⁴, (rk)⁴, (rk³)⁴, leads back to the starting vertex with no bean.


Fig. 8

This Cayley diagram is invalid. At two vertices, rkrk³ leaves us with two beans; at the other two, it leaves us with none.


Fig. 9

This Cayley diagram is invalid. At half the vertices, kr has order 2, at the other half, it has order 3.

It can be converted to a valid Cayley diagram by replacing each hexagon of directed black arcs with a hexagon of alternate blue and green undirected arcs, with a suitable choice of phase.


Fig. 10

This Cayley diagram is invalid. It portrays a group whose elements have orders 1.2⁵.3¹⁰.5⁴.6¹⁰, and no such group exists. If it existed, it would be C5⋊C6.

At ten of the vertices, rk²rk²rkrk has order 1, at the other twenty, it has order 5.

This is a sub-page of Toll-bean extensions which is a sub-page of How to build groups.
More pages on groups.