The Pauli Group

Among the groups of order less than 32, the Pauli group is one of the hardest to understand. It can be regarded as any of

• (C4 × C2) ⋊ C2
• D8 ⋊ C2
• Q8 ⋊ C2

This page aims to makes the structure of the Pauli group easier to understand.

Cayley Diagrams

Fig. 1.  The Pauli group
conventionally drawn

Fig. 2.  The Pauli group
drawn using "toll stations"

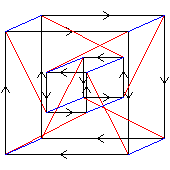
Figs. 1 & 2 are two Cayley diagrams of the Pauli group. Fig. 1 left is drawn in the usual way, and is more confusing than helpful.

Fig. 2 portrays the Pauli group as a central extension of (C2×C2×C2) by C2, using orange triangles to indicate the central extension. This use of orange triangles is described in How to Build Groups: Toll-bean Extensions. It shows a cube flattened so as to fit into two dimensions. I believe that this diagram is more useful in elucidating the structure of the Pauli group.

If we consider the faces of this cube one at at time, we can see that each face is itself a valid Cayley diagram. The left and right faces are both D8; the top and bottom faces are both C4×C2; the near and far faces are both Q8.

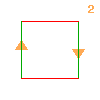
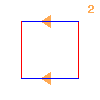
Fig. 3a.  D8	Fig. 3b.  C4×C2	Fig. 3c.  Q8

Cayley Diagrams with group elements represented as permutations

Fig. 4.  The Pauli group
with each element expressed as a permutation

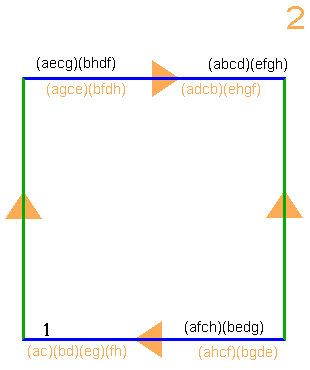
We can delete all but one of the faces of the cube shown in Fig. 4, to obtain any one of Figs. 5a, 5b, and 5c. So the Pauli group has each of D8, Q8, and C4×C2 in it as a normal subgroup of index 2. It is as if the Pauli group can be built by taking six squares, two each of Figs. 3a, 3b and 3c, and welding them together edge-to-edge to form a cube, while preserving the properties of the groups portrayed by the separate square faces.

Fig. 5a. (above): D8. Fig. 5b. (top right): Q8. Fig. 5c. (right): C4×C2.