Regular Maps in the Torus
square faces |
hexagonal faces |
triangular faces
This page shows some of the regular maps that can be drawn on the genus-1
orientable manifold, the torus. All those with 50 or fewer faces, and their duals, are
shown. For the purpose of these pages, a "regular map" is defined
here.
For other oriented manifolds, the number of such figures is small, but for the torus,
it is infinite. A reason why there are so many for the torus, and a finite number for
every other oriented 2-manifold, is that the torus has an Euler characteristic of 0.
Thus, once we have found one regular map, we can stitch together several copies
of it, to form another which still fits on a torus.
As the "curvature" of the torus is 0, its vertices must be "flat": if they are also fully
symmetrical, they must be formed from four squares, or three hexagons, or six triangles.
Infinitely many regular maps of each of these three types exist.
Regular Maps with Four Squares meeting at each Vertex:
Schläfli symbol {4,4}(a,b)
There is one regular map with four squares meeting at each vertex for each pair of
non-negative integers a,b (except for 0,0). Each has a number of faces equal to
a2+b2. Regular maps for integer pairs a,b with a<b exist,
but are not shown here; they are the enantiomorphs of those for b,a.
All these regular maps are all self-dual.
The notation {4,4}(a,b) is consistent with that used in ARM, page 18.
ARM disallows (in our notation) {4,4}(1,0), in which the single square
shares two edges with itself; and {4,4}(1,1), in which each of the two
squares shares each of its vertices (but no edge) with itself.
Any {4,4} can be cantellated, yielding a {4,4} with twice as many
vertices, faces and edges.
Regular Maps with Three Hexagons meeting at each Vertex:
Schläfli symbol {6,3}(a,b)
The regular maps with three hexagons meeting at each vertex are more complicated. They can
all be generated from pairs of number of the form a,b where a and b are either
both odd or both even. The number of faces of these regular maps is given by
(a2+3*b2)/4.
More than one such pair can generate the same regular regular map, for example {6,3}(2,4),
{6,3}(5,3), and {6,3}(7,1) are all the same regular map, with 13 faces. I have
arbitrarily chosen to list them in ascending order of the first parameter, which is necessarily also
descending order of the second parameter.
Most of these regular map are chiral, and so occur as enantiomorphic pairs. Only one (arbitrarily
chosen) member of each such pair is shown.
The notation {6,3}(a,b) used here is not consistent with
that used in ARM, page 19. Where ARM writes {6,3}(s,0) we write
{6,3}(s,s), and where ARM writes {6,3}(s,s) we write {6,3}(0, 2s).
ARM disallows regular maps which (in our notation) are not of either of the forms
{6,3}(s,s) and {6,3}(0, 2s), because they lack "full reflexional symmetry",
i.e. they are chiral. It also disallows (in our notation) {6,3}(1,1),
in which the single hexagon shares three edges with itself.
Regular Maps with Six Triangles meeting at each Vertex:
Schläfli symbol {3,6}(a,b)
The regular maps with six triangles meeting at each vertex are the duals of those with three
hexagons. As for {6,3}(a,b), a and b must be either both odd or both even.
The number of faces of these polyhedra is given by (a2+3*b2)/2.
The notation used here {3,6}(a,b) is not consistent with that used in
ARM, and is as described above for {6,3}(a,b). Thus our
{6,3}(a,b) is the dual of our {3,6}(a,b).
ARM also disallows (in our notation) {3,6}(1,1), in which each of the two triangles
shares each of its vertices (but no edge) with itself.
| designation | no. of
squares | picture | V
F
E
Eu | dual
Petrie dual | rotational
symmetry
group | comments |
|---|
| {4,4}(1,0) | 1 |  | 1
1
2
0 | self-dual
hemi-2-hosohedron | C4 |
  |
|---|
| {4,4}(1,1) | 2 |  | 2
2
4
0 | self-dual
4-hosohedron | D8 |
 |
|---|
| {4,4}(2,0) | 4 |  | 4
4
8
0 | self-dual
self-Petrie dual | C22⋊C4 | K4,4 |  |
|---|
| {4,4}(2,1) | 5 |  | 5
5
10
0 | self-dual
| Frob20
≅
C5⋊C4 | K5 
|
|---|
| {4,4}(2,2) | 8 |  | 8
8
16
0 | self-dual
self-Petrie dual | ? | |
|---|
| {4,4}(3,0) | 9 |  | 9
9
18
0 | self-dual
| C32⋊C4 | |
|---|
| {4,4}(3,1) | 10 |  | 10
10
20
0 | self-dual
| (C5⋊C4)×C2 |  |
|---|
| {4,4}(3,2) | 13 |  | 13
13
26
0 | self-dual
| C13⋊C4 |  |
|---|
| {4,4}(4,0) | 16 |  | 16
16
32
0 | self-dual
| C42⋊C4 | |
|---|
| {4,4}(4,1) | 17 |  | 17
17
34
0 | self-dual
| C17⋊C4 |  |
|---|
| {4,4}(3,3) | 18 |  | 18
18
36
0 | self-dual
| ? | |
|---|
| {4,4}(4,2) | 20 |  | 20
20
40
0 | self-dual
| ? |  |
|---|
| {4,4}(4,3) | 25 |  | 25
25
50
0 | self-dual
| ? |  |
|---|
| {4,4}(5,0) | 25 |  | 25
25
50
0 | self-dual
| C52⋊C4 | |
|---|
| {4,4}(5,1) | 26 |  | 26
26
52
0 | self-dual
| ? |  |
|---|
| {4,4}(5,2) | 29 |  | 29
29
58
0 | self-dual
| C29⋊C4 |  |
|---|
| {4,4}(4,4) | 32 | 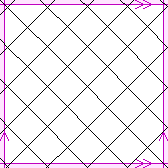 | 32
32
64
0 | self-dual
| ? | |
|---|
| {4,4}(5,3) | 34 |  | 34
34
68
0 | self-dual
| ? |  |
|---|
| {4,4}(6,0) | 36 |  | 36
36
72
0 | self-dual
| ? | |
|---|
| {4,4}(6,1) | 37 |  | 37
37
74
0 | self-dual
| C37⋊C4 |  |
|---|
| {4,4}(6,2) | 40 |  | 40
40
80
0 | self-dual
| ? |  |
|---|
| {4,4}(5,4) | 41 |  | 41
41
82
0 | self-dual
| ? |  |
|---|
| {4,4}(6,3) | 45 |  | 45
45
90
0 | self-dual
| ? |  |
|---|
| {4,4}(7,0) | 49 |  | 49
49
98
0 | self-dual
| C72⋊C4 | |
|---|
| {4,4}(7,1) | 50 |  | 50
50
100
0 | self-dual
| C50⋊C4 |  |
|---|
| {4,4}(5,5) | 50 |  | 50
50
100
0 | self-dual
| ? | |
|---|
| | no. of
hexagons | |
|---|
| {6,3}(1,1) {6,3}(2,0) | 1 |  | 2
1
3
0 | {3,6}(1,1)
3-hosohedron | D6 |
  |
|---|
| {6,3}(0,2) {6,3}(3,1) | 3 |  | 6
3
9
0 | {3,6}(0,2)
self-Petrie dual | D6×C3 | K3,3 Water, gas, and electricity
The three-rung Möbius ladder S86. |
|---|
| {6,3}(2,2) {6,3}(4,0) | 4 |  | 8
4
12
0 | {3,6}(2,2)
cube | S4 | |  |
|---|
| {6,3}(1,3) {6,3}(4,2) {6,3}(5,1) | 7 |  | 14
7
21
0 | {3,6}(1,3)
S3{14,3} | Frob42
≅
C7⋊C6 |  |
|---|
| {6,3}(3,3) {6,3}(6,0) | 9 |  | 18
9
27
0 | {3,6}(3,3)
self-Petrie dual | ? | the Pappus graph |
|---|
| {6,3}(0,4) {6,3}(6,2) | 12 | 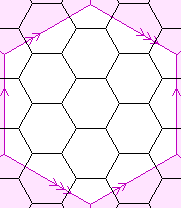 | 24
12
36
0 | {3,6}(0,4)
S4{12,3} | ? | the Nauru graph |
|---|
| {6,3}(2,4) {6,3}(5,3) {6,3}(7,1) | 13 |  | 26
13
39
0 | {3,6}(2,4)
| ? | the F26A graph 
|
|---|
| {6,3}(4,4) {6,3}(8,0) | 16 |  | 32
16
48
0 | {3,6}(4,4)
S3{8,3} | ? | The Dyck graph |
|---|
| {6,3}(1,5) {6,3}(7,3) {6,3}(8,2) | 19 |  | 38
19
57
0 | {3,6)(1,5)
| C19⋊C3 |  |
|---|
| {6,3}(3,5) {6,3}(6,4) {6,3}(9,1) | 21 |  | 42
21
63
0 | {3,6)
(3,5} | ? |  |
|---|
| {6,3}(5,5) {6,3}(10,0) | 25 |  | 50
25
75
0 | {3,6}(5,5)
| ? | |
|---|
| {6,3}(0,6) {6,3}(9,3) | 27 | 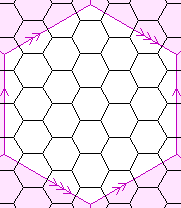 | 54
27
81
0 | {3,6}(0,6)
| ? | |
|---|
| {6,3}(2,6) {6,3}(8,4) {6,3}(10,2) | 28 |  | 56
28
84
0 | {3,6}(2,6)
| ? |  |
|---|
| {6,3}(4,6) {6,3}(7,5) {6,3}(11,1) | 31 |  | 62
31
93
0 | {3,6}(4,6)
| ? |  |
|---|
| {6,3}(6,6) {6,3}(12,0) | 36 |  | 72
36
108
0 | {3,6}(6,6)
| ? | |
|---|
| {6,3}(1,7) {6,3}(10,4) {6,3}(11,3) | 37 |  | 74
37
111
0 | {3,6}(1,7)
| ? |  |
|---|
| {6,3}(3,7) {6,3}(8,6) {6,3}(9,5) {6,3}(12,2) | 39 |  | 78
39
117
0 | {3,6}(3,7)
| ? | 
|
|---|
| {6,3}(5,7) {6,3}(13,1) | 43 |  | 86
43
126
0 | {3,6}(5,7)
| ? |  |
|---|
| {6,3}(0,8) {6,3}(12,4) | 48 | 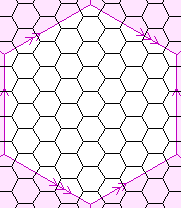 | 96
48
144
0 | {3,6}(0,8)
| ? | |
|---|
| {6,3}(7,7) {6,3}(14,0) | 49 |  | 98
49
147
0 | {3,6}(7,7)
| ? | |
|---|
| {6,3}(2,8) {6,3}(11,5) {6,3}(13,3) | 49 | 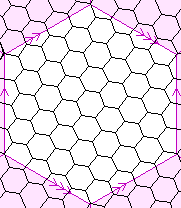 | 98
49
147
0 | {3,6}(2,8)
| ? |  |
|---|
| | no. of
triangles | |
|---|
| {3,6}(1,1} {3,6}(2,0) | 2 |  | 1
2
3
0 | {6,3}(1,1)
hemi-3-hosohedron | D6 |
 |
|---|
| {3,6}(0,2) {3,6}(3,1) | 6 |  | 3
6
9
0 | {6,3}(0,2)
C5{6,6} | D6×C3 | |
|---|
| {3,6}(2,2) {3,6}(4,0) | 8 |  | 4
8
12
0 | {6,3}(2,2)
C4{4,6} | S4 | |
|---|
| {3,6}(1,3) {3,6}(4,2) {3,6}(5,1) | 14 |  | 7
14
21
0 | {6,3}(1,3}
| Frob42
≅
C7⋊C6 | K7 
|
|---|
| {3,6}(3,3) {3,6}(6,0) | 18 |  | 9
18
27
0 | {6,3}(3,3)
| ? | K3,3,3 |
|---|
| {3,6}(0,4) {3,6}(6,2) | 24 |  | 12
24
36
0 | {6,3}(0,4)
| ? | |
|---|
| {3,6}(2,4) {3,6}(5,3) {3,6}(7,1) | 26 |  | 13
26
39
0 | {6,3}(2,4)
| ? | the Paley order-13 graph 
|
|---|
| {3,6}(4,4) {3,6}(8,0) | 32 |  | 16
32
48
0 | {6,3}(4,4)
| ? | the Shrikhande graph |
|---|
| {3,6}(1,5) {3,6}(7,3) {3,6}(8,2) | 38 |  | 19
38
57
0 | {6,3}(1,5)
| C19⋊C3 |  |
|---|
| {3,6}(3,5) {3,6}(6,4) {3,6}(9,1) | 42 |  | 21
42
63
0 | {6,3}(3,5)
| ? |  |
|---|
| {3,6}(5,5) {3,6}(10,0) | 50 |  | 25
50
75
0 | {6,3}(5,5)
| ? | |
|---|
The following figures have more than 50 faces; they are included because their duals are above. |
| {3,6}(0,6) {3,6}(9,3) | 54 |  | 27
54
81
0 | {6,3}(0,6)
| ? | |
|---|
| {3,6}(2,6) {3,6}(8,4) {3,6}(10,2) | 56 |  | 28
56
84
0 | {6,3}(2,6)
| ? |  |
|---|
| {3,6}(4,6) {3,6}(7,5) {3,6}(11,1) | 62 |  | 31
62
93
0 | {6,3}(4,6)
| ? |  |
|---|
| {3,6}(6,6) {3,6}(12,0) | 72 |  | 36
72
108
0 | {6,3}(6,6)
| ? | |
|---|
| {3,6}(1,7) {3,6}(10,4) {3,6}(11,3) | 74 |  | 37
74
111
0 | {6,3}(1,7)
| ? |  |
|---|
| {3,6}(3,7) {3,6}(8,6) {3,6}(9,5) {3,6}(12,2) | 78 |  | 39
78
117
0 | {6,3}(3,7)
| ? |  |
|---|
| {3,6}(5,7) {3,6}(13,1) | 86 |  | 43
86
126
0 | {6,3}(5,7)
| ? |  |
|---|
| {3,6}(0,8) {3,6}(12,4) | 96 |  | 48
96
144
0 | {6,3}(0,8)
| ? | |
|---|
| {3,6}(7,7) {3,6}(14,0) | 98 | 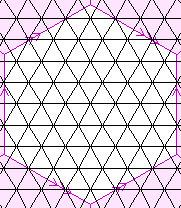 | 49
98
147
0 | {6,3}(7,7)
| ? | |
|---|
| {3,6}(2,8) {3,6}(11,5) {3,6}(13,3) | 98 |  | 49
98
147
0 | {6,3}(2,8)
| ? |  |
|---|
The pink lines, arrows, and shading are explained by the page
Representation of 2-manifolds.








































































































