Each face shares all its vertices with itself. Some readers
may consider that this invalidates it as a regular map.
This regular map has two octagonal faces, four vertices, and eight edges.
Its Petrie polygons are Eulerian octagons. Its holes are digons.
Its rotational symmetry group is the quasidihedral group of order 16.
Its dual is {4,8}. Its double cover is S3:{8,4}. It is the result of cantellating S2:{8,8}.
Each face shares all its vertices with itself. Some readers
may consider that this invalidates it as a regular map.
The picture to the left is not a regular map. Some of its Petrie polygons are digons, some are squares.
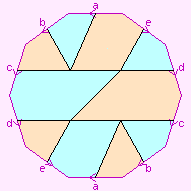
Other regular maps on the genus-2 oriented surface.
Index to other pages on regular maps.
Some pages on groups
Copyright N.S.Wedd 2009