A Non-Regular Map C⁴:{3,18}

The figure shown and described here is not a regular map. This is most evident from its 9th-order holes (obtained by travelling along the edges and taking the middle exit every time we reach a vertex): some of its 9-th order holes have one edge, some have two.

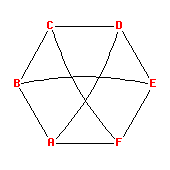
This irregular map has one 18-valent vertices, six triangular faces, and nine edges.

Its rotational symmetry group is D6.

Its dual is C¹:{18,3}.

Its Petrie polygons have 4 or 6 edges, and its holes have 18 edges.

This irregular map has edges which join a vertex to itself. You may threfore consider that it does not qualify as an irregular map.

If a regular map with one vertex and six triangular faces exists, each face must border three distinct other faces (if they are all the same the map is not connected, and if just some of them are the same it is not edge-transitive).

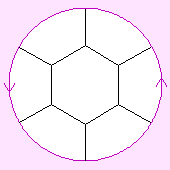
So we need to find an adjacency graph for the six faces. It must have six three-valent vertices and be regular. Various adjacency graphs for the six faces are possible, but none is regular. The closest we can get are the trangular prism with two triangular and four square faces, and the hexagonal hemiprism with one hexagonal and three square faces. Two versions of the latter are shown to the left.

The map and its adjacency graph are dual. If no regular adjacency graph exists, no regualr map exists. So no regular map {3,18) in genus 2 or genus 1cc can exist.

In this case, if we had found a regular adjacency graph, we would want a way to construct the regular map from it. So consider the order in which we visit the faces as we go around the vertex of the map. The order must correspond to a double Eulerian circuit of this graph, traversing each edge once in each direction, and never reversing immediately back over an edge as this would violate the condition that each triangle has three distinct neighbours.

To find a double Eulerian circuit that is as regular as possible, it helps to redraw the adjacency graph, making it into a map (ideally a regular map, but in this case not quite regular). In this case we find, for either the triangular prism or the hexagonal hemiprism, that its Petrie polygon (it has only one) works as a regular double-Eulerian circuit. For the hexagonal hemiprism, it visits the vertices of the graph to the left (corresponding to triangular faces of the regular map we are looking for) in the order ABC FAB EFA DEF CDE BCD. We find that we can indeed arrange the six triangles around a vertex in this order, giving the regular-looking map at the top of this page.