A Genus-C⁴ Regular Map {4,6}

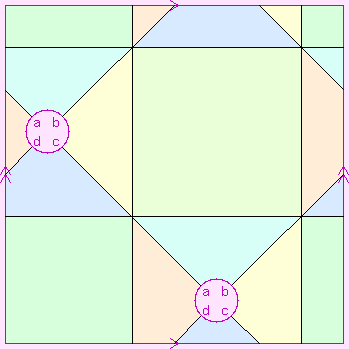
This regular map has six square faces, four 6-valent vertices, and 12 edges. Each face borders four distinct other faces (i.e. its face-multiplicity is 1), and each vertex is connected by two edges to each of the other vertices (i.e. its vertex-multiplicity is 2).

Its rotational symmetry group has order 48.

Its dual is C⁴:{6,4}₃.

Its Petrie polygons have three edges, its holes have four edges, its 2nd-order Petrie polygons have six edges, and its 3rd-order holes have 2 edges.

Its Petrie dual is S¹{3,6}_(2,2)

The image to the left shows how it can be constructed as a shuriken of the cube.

Two more versions are shown below.