Other regular maps on the genus-C4 non-oriented surface.
Index to other pages on regular maps.
Some pages on groups
Copyright N.S.Wedd 2009,2010

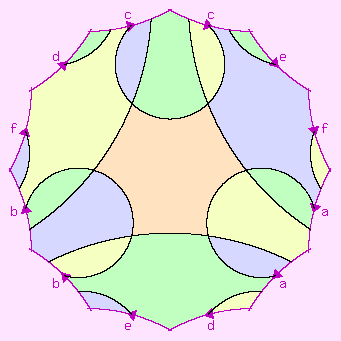
This regular map has four hexagonal faces, six 4-valent vertices, and 12 edges. Each face borders each other face twice (i.e. its face-multiplicity is 2), and each vertex is connected by two edges to each of two other edges (i.e. its vertex-multiplicity is also 2).
Its dual is C4{4,6}6. It is self-Petrie dual.
Its rotational symmetry group has order 48.
Its Petrie polygons are hexagons, and its holes are squares.
Two more portrayals of it are below.

Other regular maps on the genus-C4 non-oriented surface.
Index to other pages on regular maps.
Some pages on groups
Copyright N.S.Wedd 2009,2010