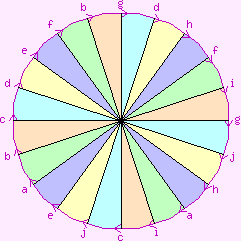
This is not a regular map. It is in genus-C6 (a sphere plus six crosscaps). It has five square faces, each meeting two of the others twice each. It has one vertex and 10 edges, giving a Euler characteristic of -4.
Its dual is C6:{20,4}.
It has one Petrie polygon with 10 edges and two each with five edges. Each edge participates in the 10-sided Petrie polygon and in one five-sided one. Its holes have two edges.
Each face shares all its vertices with itself. The edges join a vertex to itself.
Some readers may consider that this invalidates it as a regular map.
If we choose any one face in the diagram, and remove it and its four edges, we get the regular map S3:{12,12}.
This map is similar in some respects to the above. Its Petrie polygons all have five edges, and its holes both have ten.
Its dual is C6:{20,4}.
Other regular maps on the genus-C6 surface.
Index to other pages on regular maps.
Copyright N.S.Wedd 2009