Philosophy

These pages describe "regular maps", objects lying somewhere between graphs, and polyhedra. This page aims to show the relationship between graphs, regular maps, and polyhedra.

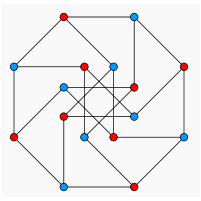
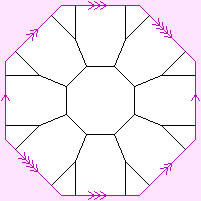
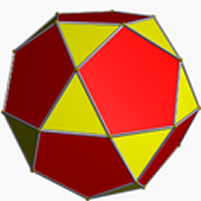
A graph is a collection of vertices and lines, joined up in a specified way, but not "in" any kind of space. A regular map is a graph that has been constrained to fit in a 2-manifold, which it partitions into faces. A polyhedron is a regular map whose 2-manifold is the 2-sphere, which has been embedded in Euclidean 3-space, so as to impose a nice metric on it; the polyhedron can then be regarded as a 3-dimensional solid object.

These differences are described further in the table below.

	Graphs	Regular Maps	Polyhedra (and Polytopes)
components	Vertices and edges	Vertices, edges, and faces	Vertices, edges, and faces (and n-faces)
embedding	Not embedded	Embedded in a 2-manifold	Embedded in Euclidean 3-space (n-space)
each one is defined by	An incidence table of vertices and edges	Incidence tables of vertices, edges and faces; and an indication of how these can be threaded through the tunnels of the manifold.	A set of vertices in Euclidean 3-space (n-space). Simpler polyhedra (polytopes) can be defined as the convex hull of such a set of vertices. Star polyhedra (polytopes) require something more, which may be incidence tables.
metric	No metric	It is sometimes possible to impose a metric	The Euclidean metric of the embedding space
how to draw them on paper or computer screen	How you like, with the arcs crossing as you wish	The arcs can't cross. The diagram will include "sewing instructions" appropriate to the manifold	Typically by a projection of an opaque space-filling object
a typical regular specimen

Higher dimensions

The "Polyhedra" column also mentions polytopes, in brackets. Could the middle column similarly mention 3-manifolds, and higher manifolds?

It could, and I am sure the non-sphere analogues of polytopes are interesting. But I suspect that listing polytope-analogues for 3-manifolds other than the 3-sphere would be very difficult. Even listing 3-manifolds is difficult.