This site includes Cayley diagrams and other things drawn on surfaces of genus 1 (toruses), and on other surfaces of higher genus. These are shown on your flat computer screen by using pink lines and symbols. The purpose of this page is to explain how to interpret these pink lines and symbols.
For those already acquainted with 2-manifolds other than the plane, this paragraph may be sufficient:
The Wikipedia page on Fundamental polygon, or this page on the Math of Non-Orientable Surfaces may also help. But if it is still not clear to you, please read the following.
Here ![]() inside the pink lines is
an ordinary piece of 2-space. Let's identify its left and right edges,
by sewing them together:
inside the pink lines is
an ordinary piece of 2-space. Let's identify its left and right edges,
by sewing them together: ![]() . This
gives us a cylinder. Or we could sew the opposite edges togther with
a half-twist:
. This
gives us a cylinder. Or we could sew the opposite edges togther with
a half-twist: ![]() . This gives us a
Möbius
strip. We can also sew both pairs of opposite edges. There are
three different ways to do this:
. This gives us a
Möbius
strip. We can also sew both pairs of opposite edges. There are
three different ways to do this: ![]() is a
torus,
is a
torus,
![]() is a
Klein bottle, and
is a
Klein bottle, and
![]() is a
projective plane.
is a
projective plane.
For the torus, I use a slightly different diagram from the above:
![]() .
.
 This differs from
This differs from
![]() in two ways. First I have extended the
lines so that they cross each other and reach the edge of the diagram, like
this
in two ways. First I have extended the
lines so that they cross each other and reach the edge of the diagram, like
this ![]() . This is because the torus,
"unrolled" onto the plane, will look like the diagram to the right, and if
we take a piece of the diagram to the right, we see the lines crossing. The
second difference is that I have used light pink to shade the parts of the
diagram which are copies of what is within the pink borders. Thus there is
a one-to one correspondence between the torus itself and the non-pink
regions of the diagram.
. This is because the torus,
"unrolled" onto the plane, will look like the diagram to the right, and if
we take a piece of the diagram to the right, we see the lines crossing. The
second difference is that I have used light pink to shade the parts of the
diagram which are copies of what is within the pink borders. Thus there is
a one-to one correspondence between the torus itself and the non-pink
regions of the diagram.



I have now explained the three diagrams above (the first two are Cayley diagrams, the third one is not). Look at them, and see how the edges which are meant to match up are indeed crossed by identical parts of the diagram.
 I also use diagrams like this:
I also use diagrams like this:  . Here,
the left and right ends join up in a simple way. But the left half of the
. Here,
the left and right ends join up in a simple way. But the left half of the
 bottom edge matches the right half of the top edge, and vice versa. This is
again a torus, one which when "unrolled" over the plane looks like the diagram
to the right.
I also use diagrams like this:
bottom edge matches the right half of the top edge, and vice versa. This is
again a torus, one which when "unrolled" over the plane looks like the diagram
to the right.
I also use diagrams like this:  . Here,
each edge of the hexagon is identified with its opposite edge. This again
a torus, though this is less obvious. When "unrolled" over the plane it
looks like the diagram to the left.
. Here,
each edge of the hexagon is identified with its opposite edge. This again
a torus, though this is less obvious. When "unrolled" over the plane it
looks like the diagram to the left.

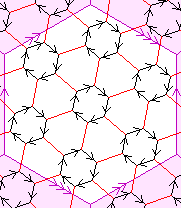

I have now explained the three diagrams above (again, the first two are Cayley diagrams, the third one is not). Look at them, and see how the edges which are meant to match up indeed do, and how, in the last two, fairly large regions of the white torus are repeated in the light pink regions.
Suppose we want to add a "handle" to a diagram. Think of a teapot handle. We want to take such a handle, with the cut surfaces of its two ends lying in the same plane, and glue it onto our surface. Here is how we do it.
The places where the handle is glued on won't be part of the diagram any more,
and we will show them in light pink, surrounded by pink circles where the
surface of the handle is attached. We won't actually show the handle itself;
but to show how the two ends of it match up, we will use letters to show
what corresponds to what. This means that we can't have any interesting bits
of the diagram actually on the handle, just line which run form end to end
of the handle, possibly spiralling round as they go. Here is what the two ends
of the handle might look like: ![]() and
and
![]() . Note that the letters go clockwise
around one, anticlockwise around the other, as required by the nature of a handle.
. Note that the letters go clockwise
around one, anticlockwise around the other, as required by the nature of a handle.

You should now be able to interpret the Cayley diagram above.


The handles described above bend through 180°. This is why the labels on their two ends run in opposite directions. Another way of adding a handle to a surface is to have a handle that goes from the back of the image and bends through 360° all the way round to the front. This is illustrated be the two diagrams to the right, which are each of a torus. As it a 360° bend, the symbols appear in the same order at the two ends of the handle. There may be a twist to the handle, as in the second of the two diagrams to the right.

Such diagrams are little use in themselves, they are just another way to draw
a torus. But they may be useful with more handles added, as in the diagram to
the left, which has three handles, and is therefore of a surface of genus 3.
t.png)

You should now be able to interpret the two diagrams above. If you click on either you will see a full-sized version of it. The first one is a Cayley diagram, the second one is a regular map.

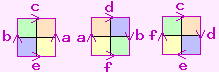
There is no need for the non-pink region to be connected. The first diagram to the right gives sewing instructions for Fortunatus's purse, described below. The second uses this version of the projective plane to portray a hemi-octahedron, with four triangular faces.
In some diagrams, for non-orientable manifolds, I use crosscaps, shown like
this ![]() . Any two
points directly across a crosscap from each other are identified with each
other.
. Any two
points directly across a crosscap from each other are identified with each
other.
This site, and even this page, make it clear that there can be many different diagrams that correspond to the same manifold. Which one you choose to use can depend on what you want to do with it. The page Choosing a way to represent a 2-manifold gives guidance on how to choose a suitable diagram.
I use the term "sewing" for the process of constructing a 2-manifold, because it is the first term I encountered for it. In Sylvie and Bruno Concluded ARM by Lewis Carroll, chapter 7 "Mein Herr", there is a description of how to sew a Fortunatus's purse from three pocket handkerchiefs.
The character "Mein Herr" describes the process. You take three square handkerchiefs. You sew two together along one edge, and then again along the opposite edges to those already sewn, but with a half-twist, to make a Möbius strip. You observe that it has a single edge, four handkerchief-sides long, just like the so far unused third handkerchief. You then sew the Möbius strip to the third hankerchief all along its edge.
If this final manoeuvre were physically possible, it would result in a projective plane. However a projective plane cannot be embedded in 3-space without self-intersection, and trying to sew a self-intersecting surface results in a mess. Self-intersecting surfaces, including the projective plane, can however be knitted.
Regular maps drawn in various 2-manifolds
Cayley graphs drawn in various 2-manifolds.
Copyright N.S.Wedd 2009