
This regular map is in genus-6c (a sphere plus six crosscaps). It has six decagonal faces, each meeting each of the others twice. It has 20 vertices and 30 edges, giving a Euler characteristic of -4.
Its graph is the Desargues graph.
Its dual is C6:{3,10}.
Its rotational symmetry group is S5.
Its Petrie polygons have 10 edges. It is its own Petrie dual.
It is different from C6:{10,3}5. C6:{10,3}10 has a girth (minimal loop) of six edges, C6:{10,3}5 has a girth of five.
The vertices form antipodal pairs. The edges form antipodal pairs. Each face is antipodal to a Petrie polygon.
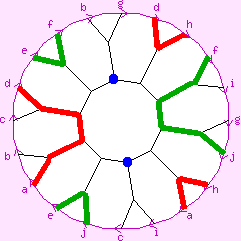
There are hexagons formed by traversing the edges and turning left, left, right, right, left, left, right, right, etc., at successive vertices. Each such hexagon is antipodal to another such hexagon and to two faces. The diagram to the left show an antipodal set of two of these hexagons and two vertices.
Other regular maps on the genus-6c oriented surface.
Index to other pages on regular maps.
Copyright N.S.Wedd 2009