An example of constructing a double cover of a Regular Map

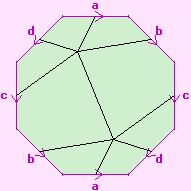
This page explains in detail how to take a particular regular map, S²:{10,5}, shown to the right, and construct its double cover.

S²:{10,5} has one decagonal face, two vertices, and five edges. Thus its Euler number is -2, and it is of genus 2. We will construct a double cover of it, which will have two decagonal face, four vertices, and ten edges. This will have Euler number -4, and be of genus 3.

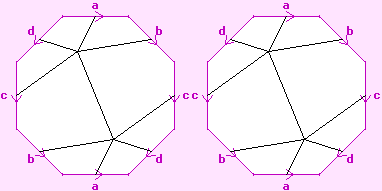
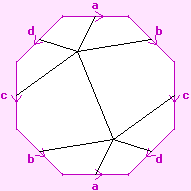
First, we remove its face-colouring, as shown to the left. This is necessary because its faces won't survive the process of constructing the double cover.

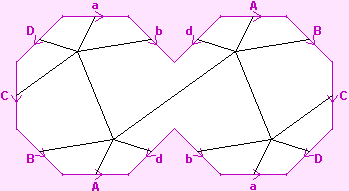
Then we take a second copy of it, and put this alongside, as shown to the right.

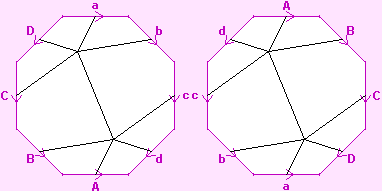
Now each of the edge labels appears four times in the diagram. We correct this by modifying one of each letter from lower-case to upper-case in the left twin; and modifying the other copy of that letter from lower-case to upper-case in the right twin. The result is shown to the right.

What we now have is the required double cover.

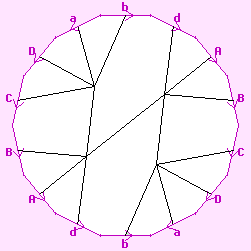
There is some more tidying-up we can do. First we push the two octagons togeher, so that they meet, along the edge labelled "c". This gives the diagram to the right. Now we have a 14-gon. We redraw this, just bending the angles but not changing anything, so as to give a regular 14-gon as shown to the left.

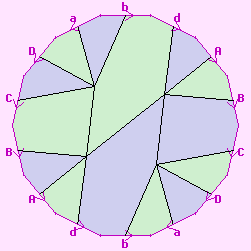
Now we colour the faces, to make it clearer what has happened, as shown to the right. We now have a map S³:{10,5} with two decagonal faces, four valence-5 vertices, and ten edges, as expected.

Unfortunately, though we started with a regular map, the double cover is not a regular map. Eight of its ten edges are common to the two faces, and two of them are not: so it is not edge-transitive.