Pyritification of {8,4}

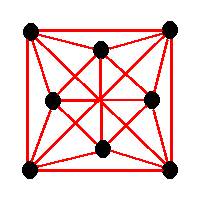
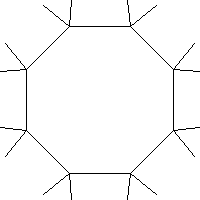
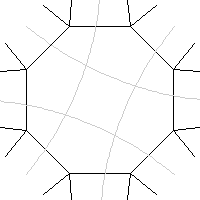
Take an octagon, forming part of a {8,4} regular map, as shown to the left. Divide it up, as shown by the grey lines in the diagram to the right. It is converted to four pentagons and five squares.

If we have a regular map with octagonal faces, and we apply this process to it, we don't get a regular map, the result is not face-transitive. It is "quasiregular", being vertex-transitive and edge-transitive, but not face-transitive nor half-edge-transitive. A quasiregular polyhedron has two kinds of regular face, which alternate in a chequerboard fashion. We have converted our octagonal-faced regular map to a chequer-board of pentagons and squares, a quasiregular map, as seen to the right.

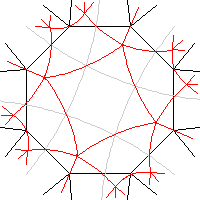
We can make this quasiregular map into a regular-looking map {5,4} by getting rid of the squares, partitioning the territory of each among its four neighbouring pentagons. The result is shown to the left (ignore the grey edges and the black edges, just consider the red edges).

Alternatively, we can make the dual regular-looking map {4,5} by partitioning the territory of each pentagon among its five neighbouring squares. This is shown to the right in the same way.

Unfortunately, while the resulting maps look regular, they are not. They lack five-fold rotational symmetry. The adjacency graph of the faces of S²{5,4} is shown below: its symmetry group is D8.