A Series of Group Presentations

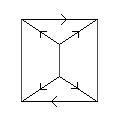
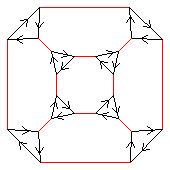
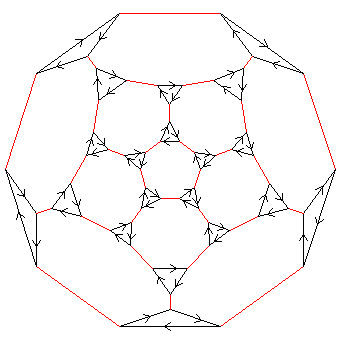
Consider the presentation

    < k, r | k³, r², (kr)ⁿ >

for n = 2, 3, 4, 5. The groups generated are S3, A4, S4, A5 respectively. These are illustrated below.

n	Presentation	Group	Cayley graph
2	< k, r | k3, r2, (kr)2 >	S3
3	< k, r | k3, r2, (kr)3 >	A4
4	< k, r | k3, r2, (kr)4 >	S4
5	< k, r | k3, r2, (kr)5 >	A5

Unfortunately the series S3,A4,S4,A5 does not extend at each end, giving A3,S3,A4,S4,A5,S5,A6, etc., as we might have hoped.

The preceding presentation for n=1 < k, r | k³, r², (kr)¹ > generates, not A3, but the one-element group.

The subsequent presentation for n=6 < k, r | k³, r², (kr)⁶ > generates, not S6, but an infinite group, containing ℤ×ℤ, part of whose Cayley graph is .

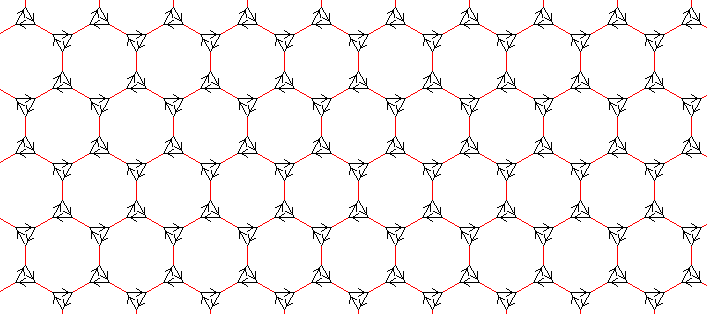For n>6, < k, r | k³, r², (kr)⁷ > etc. give infinite groups, whose Cayley diagrams can be drawn nicely in the hyperbolic plane, and which have free groups as subgroups.

For n=ω, < k, r | k³, r² > gives PSL(2,ℤ).

More miscellaneous short pages on finite groups
More pages on groups

Copyright N.S.Wedd 2008