 Suppose we are calculating the Upper Central series of G:
Suppose we are calculating the Upper Central series of G:1, z(G), ..., P, Q, ...
and we have got as far as P and want to find Q.
This page explains what an "Upper Central Series" is, in terms I can understand. It was assembled from two sources 1,2 neither of which I could understand alone.
A central series is a special case of a "normal series". A normal series for a group G is a series of groups, starting with 1 and ending with G, such that each is a subgroup of the next and is a normal subgroup of G.
An Upper Central Series is generally neither upper nor a central series. Most upper central series are not central series because they never make it all the way to G. And those that do not make it to G are not "upper", because they start at 1 and include only the lower end of G.
A Lower Central Series is never a central series, and generally not lower. It is not even the right way round: it starts at G, and the groups get smaller. And like an upper central series, it generally does not make it all the way down to 1, and when it fails, it includes only the upper part of the group.
A group has a unique Upper Central Series. It is a "Normal Series" in the sense that each member is a normal subgroup of the next. The first term is the trivial group 1, and the second term is the centre of the group, z(G).
Eventually, the series will start repeating. Conventionally, one stops writing it at that point (I have not done so in the examples below). If it reaches the whole group G, then G is said to be nilpotent.
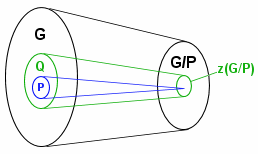
 Suppose we are calculating the Upper Central series of G:
Suppose we are calculating the Upper Central series of G:
1, z(G), ..., P, Q, ...
and we have got as far as P and want to find Q.
Consider the homomorphism G → G/P as shown to the right. Q is the normal subgroup of G which this homomorphism takes to z(G/P); i.e. the preimage of z(G/P) in G.
| C6 | 1, C6, C6, ... |
| D6 | 1, 1, ... |
| Q8 | 1, C2, Q8, Q8, ... |
| A4 | 1, 1, ... |
| Pauli | 1, C4, Pauli, Pauli, ... |
| S4 | 1, 1, ... |
| GL(2,3) | 1, C2, C2, ... |
1 John F. Humphreys. Cohomology of Finite Groups, OUP 1996, ISBN 0-19-853459-0. Page 155.
2 Wikipedia on Upper central series
More miscellaneous short pages on finite groups
More pages on groups
Copyright N.S.Wedd 2008