The Genus-3 Regular Map {12,12}

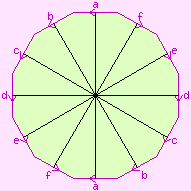
This genus-3 regular map, shown to the right, has one dodecagonal face, meeting itself twelve times at the single vertex. It has six edges, and a Euler characteristic of -4.

It is self-dual. Its Petrie dual is the 6-hemihosohedron. It can be cantellated to produce S³:{12,4}.

Its rotational symmetry group is D12.

The face shares all its vertices and all its edges with itself. The edges join a vertex to itself. Some readers may consider that this invalidates it as a regular map.

Its holes have three edges. Its Petrie polygons have two edges.

Antipodal Faces and Vertices

The face is antipodal to the vertex, and vice versa. The six edges form a single antipodal set. Rotating any one edge about its centre causes every other edge to remain where it is and rotate about its own centre: this is the involution of its rotational symmetry group.

It is possible to insert another face so as to convert this map to the regular map C⁶:{4,20}.