Regular maps in the orientable surface of genus 1

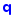
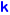
Name	Schläfli	V / F / E	mV, mF	notes	C&D no.	images	wire- frames
{4,4}(1,0)	{4,4}2	1 / 1 / 2	4,4		R1.s1-0	1	2
{6,3}(1,1)	{6,3}2	2 / 1 / 3	3,6		R1.t1-1′	5	0
{3,6}(1,1)	{3,6}2	1 / 2 / 3	6,3		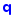R1.t1-1	2	0
{4,4}(1,1)	{4,4}2	2 / 2 / 4	4,4		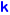R1.s1-1	6	7
{4,4}(2,0)	{4,4}4	4 / 4 / 8	2,2		R1.s2-0	4	8
{6,3}(0,2)	{6,3}6	6 / 3 / 9	1,3		R1.t0-2′	1	0
{3,6}(0,2)	{3,6}6	3 / 6 / 9	3,1		R1.t0-2	3	0
{4,4}(2,1)	{4,4}10	5 / 5 / 10	1,1		C1.s2-1	1	0
{6,3}(2,2)	{6,3}4	8 / 4 / 12	1,2		R1.t2-2′	1	0
{3,6}(2,2)	{3,6}4	4 / 8 / 12	2,1		R1.t2-2	1	0
{4,4}(2,2)	{4,4}4	8 / 8 / 16	1,1		R1.s2-2	2	2
{4,4}(3,0)	{4,4}6	9 / 9 / 18	1,1		R1.s3-0	1	0
{4,4}(3,1)	{4,4}10	10 / 10 / 20	1,1		C1.s3-1	2	0
the Heawood map	{6,3}14	14 / 7 / 21	1,1		C1.t1-3′	1	0
the dual Heawood map	{3,6}14	7 / 14 / 21	1,1		C1.t1-3	1	0
{4,4}(3,2)	{4,4}26	13 / 13 / 26	1,1		C1.s3-2	1	0
{6,3}(3,3)	{6,3}6	18 / 9 / 27	1,1		R1.t3-3′	1	0
{3,6}(3,3)	{3,6}6	9 / 18 / 27	1,1		R1.t3-3	1	0
{4,4}(4,0)	{4,4}8	16 / 16 / 32	1,1		R1.s4-0	1	0
{4,4}(4,1)	{4,4}34	17 / 17 / 34	1,1		C1.s4-1	1	0
{6,3}(0,4)	{6,3}12	24 / 12 / 36	1,1		R1.t0-4′	1	0
{4,4}(3,3)	{4,4}6	18 / 18 / 36	1,1		R1.s3-3	1	0
{3,6}(0,4)	{3,6}12	12 / 24 / 36	1,1		R1.t0-4	1	0
{6,3}(2,4)	{6,3}26	26 / 13 / 39	1,1		C1.t2-4′	1	0
{3,6}(2,4)	{3,6}26	13 / 26 / 39	1,1		C1.t2-4	1	0
{4,4}(4,2)	{4,4}20	20 / 20 / 40	1,1		C1.s4-2	1	2
{6,3}(4,4)	{6,3}8	32 / 16 / 48	1,1		R1.t4-4′	1	0
{3,6}(4,4)	{3,6}8	16 / 32 / 48	1,1		R1.t4-4	1	0
{4,4}(5,0)	{4,4}10	25 / 25 / 50	1,1		R1.s5-0	1	0
{4,4}(4,3)	{4,4}50	25 / 25 / 50	1,1		C1.s4-3	1	0
{4,4}(5,1)	{4,4}26	26 / 26 / 52	1,1		C1.s5-1	1	0
{6,3}(1,5)	{6,3}38	38 / 19 / 57	1,1		C1.t1-5′	1	0
{3,6}(1,5)	{3,6}38	19 / 38 / 57	1,1		C1.t1-5	1	0
{4,4}(5,2)	{4,4}58	29 / 29 / 58	1,1		C1.s5-2	1	0
{6,3}(3,5)	{6,3}42	42 / 21 / 63	1,1		C1.t3-5′	1	0
{3,6}(3,5)	{3,6}42	21 / 42 / 63	1,1		C1.t3-5	1	0
{4,4}(4,4)	{4,4}8	32 / 32 / 64	1,1		R1.s4-4	1	0
{4,4}(5,3)	{4,4}34	34 / 34 / 68	1,1		C1.s5-3	1	0
{4,4}(6,0)	{4,4}12	36 / 36 / 72	1,1		R1.s6-0	1	0
{4,4}(6,1)	{4,4}74	37 / 37 / 74	1,1		C1.s6-1	1	0
{6,3}(5,5)	{6,3}10	50 / 25 / 75	1,1		R1.t5-5′	1	0
{3,6}(5,5)	{3,6}10	25 / 50 / 75	1,1		R1.t5-5	1	0
{4,4}(6,2)	{4,4}20	40 / 40 / 80	1,1		C1.s6-2	1	0
{6,3}(0,6)	{6,3}18	54 / 27 / 81	1,1		R1.t0-6′	1	0
{3,6}(0,6)	{3,6}18	27 / 54 / 81	1,1		R1.t0-6	1	0
{4,4}(5,4)	{4,4}82	41 / 41 / 82	1,1		C1.s5-4	1	0
{6,3}(2,6)	{6,3}28	56 / 28 / 84	1,1		C1.t2-6′	1	0
{3,6}(2,6)	{3,6}28	28 / 56 / 84	1,1		C1.t2-6	1	0
{4,4}(6,3)	{4,4}30	45 / 45 / 90	1,1		C1.s6-3	1	0
{6,3}(4,6)	{6,3}62	62 / 31 / 93	1,1		C1.t4-6′	1	0
{3,6}(4,6)	{3,6}62	31 / 62 / 93	1,1		C1.t4-6	1	0
{4,4}(7,0)	{4,4}14	49 / 49 / 98	1,1		R1.s7-0	1	0
{4,4}(5,5)	{4,4}10	50 / 50 / 100	1,1		R1.s5-5	1	0
{4,4}(7,1)	{4,4}50	50 / 50 / 100	1,1		C1.s7-1	1	0
{6,3}(6,6)	{6,3}12	72 / 36 / 108	1,1		R1.t6-6′	1	0
{3,6}(6,6)	{3,6}12	36 / 72 / 108	1,1		R1.t6-6	1	0
{6,3}(1,7)	{6,3}74	74 / 37 / 111	1,1		C1.t1-7′	1	0
{3,6}(1,7)	{3,6}74	37 / 74 / 111	1,1		C1.t1-7	1	0
{6,3}(3,7)	{6,3}78	78 / 39 / 117	1,1		C1.t3-7′	1	0
{3,6}(3,7)	{3,6}78	39 / 78 / 117	1,1		C1.t3-7	1	0
{4,4}(8,0)	{4,4}	64 / 64 / 128	1,1		R1.s8-0	0	0
{6,3}(5,7)	{6,3}86	86 / 43 / 129	1,1		C1.t5-7′	1	0
{3,6}(5,7)	{3,6}86	43 / 86 / 129	1,1		C1.t5-7	1	0
{6,3}(0,8)	{6,3}24	96 / 48 / 144	1,1		R1.t0-8′	1	0
{4,4}(6,6)	{4,4}	72 / 72 / 144	1,1		R1.s6-6	0	0
{3,6}(0,8)	{3,6}24	48 / 96 / 144	1,1		R1.t0-8	1	0
{6,3}(7,7)	{6,3}14	98 / 49 / 147	1,1		R1.t7-7′	1	0
{3,6}(7,7)	{3,6}14	49 / 98 / 147	1,1		R1.t7-7	1	0
{6,3}(2,8)	{6,3}98	98 / 49 / 147	1,1		C1.t2-8′	1	0
{3,6}(2,8)	{3,6}98	49 / 98 / 147	1,1		C1.t2-8	1	0
{4,4}(9,0)	{4,4}	81 / 81 / 162	1,1		R1.s9-0	0	0
{6,3}(8,8)	{6,3}	128 / 64 / 192	1,1		R1.t8-8′	0	0
{3,6}(8,8)	{3,6}	64 / 128 / 192	1,1		R1.t8-8	0	0
{4,4}(7,7)	{4,4}	98 / 98 / 196	1,1		R1.s7-7	0	0
{4,4}(10,0)	{4,4}	100 / 100 / 200	1,1		R1.s10-0	0	0
{6,3}(0,10)	{6,3}	150 / 75 / 225	1,1		R1.t0-10	0	0
{3,6}(0,10)	{3,6}	75 / 150 / 225	1,1		R1.t0-10	0	0
{4,4}(11,0)	{4,4}	121 / 121 / 242	1,1		R1.s11-0	0	0
{4,4}(8,8)	{4,4}	128 / 128 / 256	1,1		R1.s8-8	0	0
{4,4}(12,0)	{4,4}	144 / 144 / 288	1,1		R1.s12-0	0	0
{6,3}(10,10)	{6,3}	200 / 100 / 300	1,1		R1.t10-10	0	0
{3,6}(10,10)	{3,6}	100 / 200 / 300	1,1		R1.t10-10	0	0
{6,3}(0,12)	{6,3}	216 / 108 / 324	1,1		R1.t0-12	0	0
{4,4}(9,9)	{4,4}	162 / 162 / 324	1,1		R1.s9-9	0	0
{3,6}(0,12)	{3,6}	108 / 216 / 324	1,1		R1.t0-12	0	0
{4,4}(13,0)	{4,4}	169 / 169 / 338	1,1		R1.s13-0	0	0
{4,4}(14,0)	{4,4}	196 / 196 / 392	1,1		R1.s14-0	0	0
{4,4}(10,10)	{4,4}	200 / 200 / 400	1,1		R1.s10-10	0	0
{6,3}(12,12)	{6,3}	288 / 144 / 432	1,1		R1.t12-12	0	0
{3,6}(12,12)	{3,6}	144 / 288 / 432	1,1		R1.t12-12	0	0
{6,3}(0,14)	{6,3}	294 / 147 / 441	1,1		R1.t0-14	0	0
{3,6}(0,14)	{3,6}	147 / 294 / 441	1,1		R1.t0-14	0	0
{4,4}(15,0)	{4,4}	225 / 225 / 450	1,1		R1.s15-0	0	0
{4,4}(11,11)	{4,4}	242 / 242 / 484	1,1		R1.s11-11	0	0
{4,4}(16,0)	{4,4}	256 / 256 / 512	1,1		R1.s16-0	0	0
{6,3}(0,16)	{6,3}	384 / 192 / 576	1,1		R1.t0-16	0	0
{4,4}(12,12)	{4,4}	288 / 288 / 576	1,1		R1.s12-12	0	0
{3,6}(0,16)	{3,6}	192 / 384 / 576	1,1		R1.t0-16	0	0
{6,3}(14,14)	{6,3}	392 / 196 / 588	1,1		R1.t14-14	0	0
{3,6}(14,14)	{3,6}	196 / 392 / 588	1,1		R1.t14-14	0	0
{4,4}(13,13)	{4,4}	338 / 338 / 676	1,1		R1.s13-13	0	0
{6,3}(16,16)	{6,3}	512 / 256 / 768	1,1		R1.t16-16	0	0
{3,6}(16,16)	{3,6}	256 / 512 / 768	1,1		R1.t16-16	0	0
{4,4}(14,14)	{4,4}	392 / 392 / 784	1,1		R1.s14-14	0	0
{4,4}(15,15)	{4,4}	450 / 450 / 900	1,1		R1.s15-15	0	0
{4,4}(16,16)	{4,4}	512 / 512 / 1024	1,1		R1.s16-16	0	0

Other Regular Maps

General Index