Cayley Diagrams of Small Groups, drawn on the Torus

This page gives the Cayley diagrams of all the groups of order less than 32. Their presentations are also given. The letters in the presentations correspond to the colours in the Cayley diagrams: black red green blue mauve grey.

The pink lines and arrows at the edges of each diagram are sewing instructions, and the light pink region outside these lines is not really there. If the previous sentence makes no sense to you, the Wikipedia page on Fundamental polygon may help.

Notation

N ⋊ H indicates a semidirect product of N by H. N is the normal subgroup.

QN, DN and DicN denote groups of order N (the quaternion, dihedral and dicyclic groups respectively).

Cyclic groups are denoted by C.

Contents

1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31

Order   Name Presentation
generators as permutations		 Cayley diagram Orders of elements
Centre
Derived subgroup

Automorphisms
GAP no., name
(Sylow subgroup)
1 Abelian 1 <> 1
1
1

1/1=1
1, 1
2 Abelian C2 < k | k2 >
k=(ab)		 1.2
C2
1

1 / 1 = 1
1, C2
3 Abelian C3
≅ A3 		< k | k3 >
k=(abc) 		1.32
C3
1

C2 / 1 = C2
1, C3
4 Abelian C4
< k | k4 >
k=(abcd) 		1.2.42
C4
1

C2 / 1 = C2
1, C4
C2 × C2 < r,k | r2, k2, rkrk >
r=(ab)(cd) b=(ad)(bc)

< r,g,b | r2, g2, rgb >
r=(ab)(cd) g=(ac)(bd) b=(ad)(bc)

1.23
C2×C2
1

D6 / 1 = D6
2, C2 x C2
5 Abelian C5 < k | k5 >
k=(abcde) 		1.54
C5
1

C4 / 1 = C4
1, C5
6 Abelian C6
C3 × C2 		< k | k6 >
k=(abcdef)

< k,r | k3, r2, krk-1r >
k=(abc) r=(de)

1.2.32.62
C6
1

C2 / 1 = C2
2, C6
Other D6
≅S3
≅ C3 ⋊ C2 		< k,r | k3, r2, krkr >
k=(abc) r=(bc) 		1.23.32
1
C3

D6 / D6 = 1
1, S3
7 Abelian C7 < k | k7 >
k=(abcdefg) 		1.76
C7
1

C6 / 1 = 1
1, C7
8 Abelian C8 < k | k8 >
k=(abcdefgh) 		1.2.42.84
C8
1

C22 / 1 = C22
1, C8
C4 × C2 < k,r | k4, r2, krk-1r >
k=(abcd) r=(ef) 		1.21+2.44
C4×C2
1

D8 / 1 = D8
2, C4 x C2
C2 × C2 × C2 < r,g,b | r2, g2, b2, rgrg, gbgb, rbrb >
r=(ab)(cd) g=(ac)(bd) b=(ad)(bc) 		1.27
C2×C2×C2
1

PSL(3,2) / 1 = PSL(3,2)
5, C2 x C2 x C2
Other D8
= C4 ⋊ C2 		< k,r | r4, r2, krkr >
k=(abcd) r=(ac)

< r,g,b | b2, g2, r2, bgbg, rbrg, rgrb >
b=(ab)(cd) g=(ac)(bd) r=(bc)

1.21+4.42
C2
C2

D8 / C22 = C2
3, D8
Q8
a.k.a. Dic8 		< k,r | k4, r4, k2r2 >
b=(abcd)(ehgf) b=(afch)(bgde)

< r,g,b | r4, g4, b4, (rgb)2 >
r=(abde)(fhcg) g=(acdf)(egbh) b=(bcef)(agdh)

1.2.46
C2
C2

S4 / C22 = D6
4, Q8
9 Abelian C9 < k | k9 >
k=(abcdefghi) 		1.32.66
C9
1

C6 / 1 = C6
1, C9
C3 × C3 < k, r | k3, r3, krkkrr >
k=(abc) r=(def) 		1.38
C3×C3
1

GL(2,3) / 1 = GL(2,3)
2, C3 x C3
10 Abelian C10
≅ C5 × C2 		< k | k10 >
k=(abcdefghij)

< k,r | k5, r2, krk-1r  >
k=(abcde) r=(fg)

1.2.54.104
C10
1

C4 / 1 = C4
2, C10
Other D10
= C5⋊C2 		< k,r | k5, r2, krkr >
k=(abcde) r=(be)(cd) 		1.25.54
1
C5

C5⋊C4 / D10 = C2
1, D10
11 Abelian C11 < k | k11 >
k=(abcdefghijk) 		1.1110
C11
1

C10 / 1 = C10
1, C11
12 Abelian C12
≅ C4 × C3 		< k | k12 >
k=(abcdefghijkl)

< k, r | k4, r3, krkkkrr >
k=(abc) r=(defg)

1.2.32.42.62.124
C12
1

C22 / 1 = C22
2, C12
C4
C6 × C2
≅ C3 × C2 × C2 		< k,r | k6, r2, krkkkkkr >
k=(abcdef) r=(gh)

< r,g,b | r2, g2, b4, all commute >
r=(ab)(cd) g=(ac)(bd) b=(pqr)

1.23.32.66
C6×C2
1

D12 / 1 = D12
5, C6 x C2
C22
Other direct products D12
= D6 ⋊ C2
≅ D6 × C2 		< k,r | k6, r2, krkr >
k=(abcdef) r=(bf)(ce)

< r,g,b | r2, g2, b2, (rg)3, b central >

1.21+6.32.62
C2
C3

D12 / D6 = C2
4, D12
C22
Other Dic12
≅ C3 ⋊ C4 		< k,r | k6, r4, k3r2 >
b=(abc)(pr)(qs) r=(bc)(pqrs) 		1.2.32.46.62
C2
C3

D12 / D6 = C2
1, C3 : C4
C4
A4
= (C2×C2) ⋊ C3 		< k,r | k3, r3, (kr)2 > 1.23.38
1
C22

S4 / A4 = C2
3, A4
C22
13 Abelian C13 < k | k13 >
k=(abcdefghijklm) 		1.1312
C13
1

C12 / 1 = C12
1, C13
14 Abelian C14
≅ C7 × C2 		< k | k14 >
k=(abcdefghijklmn)

< k,r | k7, r2, krk6r >
k=(abcdefg) r=(pq)

1.2.76.146
C14
1

C6 / 1 = C6
2, C14
Other D14
= C7 ⋊ C2 		< k,r | k7, r2, krkr >
k=(abcdefg) r=(bg)(cf)(de) 		1.27.76
1
C7

C7⋊C6 / D14 = C3
1, D14
15 Abelian C15
≅ C5 × C3 		< k | k15 >
k=(abcdefghijklmno)

< k,r | k3, r5, krkkrrr >
k=(abcde) r=(mno)

1.32.54.158
C15
1

C4×C2 / 1 = C4×C2
1, C15
16 Abelian C16
 < k | k16 >
k=(abcdefghijklmnop) 		1.2.42.84.168
C16
1

C4×C2 / 1 = C4×C2
1, C16
C8 × C2 < k,r | k8, r2, krk-1r >
k=(abcdefgh) r=(ij) 		1.23.44.88
C8×C2
1

D8×C2 / 1 = D8×C2
5, C8 x C2
C4 × C4 < k,r | k4, r4, krk-1r-1 >
k=(abcd) r=(efgh) 		1.23.412
C4×C4
1

(C22×A4)⋊C2 / 1 = (C22×A4)⋊C2
2, C4 x C4
C4 × C2 × C2 < r,g,b | r2, g2, b4, all commute >
r=(ab) g=(cd) e=(efgh) 		1.21+6.48
C4×C2×C2
1

"(((D8×C2)⋊C2)⋊C3)⋊C2" / 1 = ?
10, C4 x C2 x C2
C2 × C2 × C2 × C2 < r,g,b,k | r2, g2, b2, k2, all commute >
r=(ab) g=(cd) b=(ef) m=(gh) 		1.215
C2×C2×C2×C2
1

A8 / 1 = A8
14, C2 x C2 x C2 x C2
Other direct products D8 × C2 < r,g,b | r2, g2, b2, (rg)4, b central > 1.21+2+8.44
C2×C2
C2

"(((C4×C2)⋊C2)⋊C2)⋊C2" / C22 = ?
11, C2 x D8
Q8 × C2 < r,b,g | r4, b4, gr, rrbb, rgr-1g, bgb-1g >
r=(abcd)(efgh) b=(aecg)(fbhd) g=(pq) 		1.21+2.412
C2×C2
C2

"(((C24)⋊C3)⋊C2)⋊C2" / C22 = ?
12, C2 x Q8
Other D16
= C8 ⋊ C2
 < k,r | k8, r2, krkr >
k=(abcdefgh) r=(bh)(cg)(df) 		1.21+8.42.84
C2
C4

"(D8×C2)⋊C2" / D8 = C22
7, D16
Modular
= C8 ⋊ C2 		< k,r | k8, r2, krkkkr >
k=(abcdefgh) r=(bf)(dh) 		1.21+2.44.88
C4
C2

D8×C2 / C22 = C22
6, (C4 x C2) : C2
Quasidihedral, a.k.a. semidihedral
= C8 ⋊ C2 		< k,r | k8, r2, krkkkkkr >
k=(abcdefgh) r=(bd)(cg)(fh) 		1.21+4.46.84
C2
C4

D8×C2 / D8 = C2
8, QD16
Dic16

a.k.a. Q16 		< k,r | k8, r4, k4r2 >
k=(abcdefgh)(pqrstuvw) r=(apet)(bwfs)(cvgr)(duhq) 		1.2.410.84
C2
C4

(D8×C2)⋊C2 / D8 = C22
9, Q16
C4 ⋊ C4 < k,r | k4, r4, krkr3 >
k=(abcd) r=(bd)(efgh) 		1.23.412
C2×C2
C2

C24⋊C2 / C22 = ?
4, C4 : C4
(C2 × C2) ⋊ C4 < r,g,k | r2, g2, k4, rgrg, krkkkg, kgkkkr >
r=(ab)(cd) g=(ac)(bd) e=(bc)(pqrs) 		1.23+4.48
C2×C2
C2

C24⋊C2 / C22 = ?
3, (C4 x C2) : C2
Pauli
= D8 ⋊ C2
= Q8 ⋊ C2
= (C4×C2) ⋊ C2 		< k,r,g | k4, r2, g2, krkr, kgkkkg, kkrgrg >
k=(abcd)(efgh) r=(bd)(eg) g=(ae)(bf)(cg)(dh) 		1.27.48
C4
C2

S4×C2 / C22 = ?
13, C4 : C4
17 Abelian C17 < k | k17 >
k=(abcdefghijklmnopq) 		1.1716
C17
1

C16 / 1 = C16
1, C17
18 Abelian C18
= C9 × C2 		< k | k18 >
k=(abcdefghijklmnopqr)

< k,r | k9, r2, krk-1r-1 >
k=(abcdefghi) r=(mn)

1.2.32.62.96.186
C18
1

C6 / 1 = C6
2, C18
C9
C6 × C3
= C3 × C3 × C2 		< k,r | k6, r3, krk-1r-1 >
k=(abcdef) r=(jkl) 		1.2.38.68
C6×C3
1

GL(2,3) / 1 = GL(2,3)
5, C6 x C3
C32
Other direct products D6 × C3

≅ (C3 × C3) ⋊ C2
with the C2 interchanging the generators of the two C3s

< r,g,b | k2, g2, b3, (rg)3, b central > 1.23.38.66
C3
C3

D12 / D6 = C2
3, C3 x S3
C32
Other D18 < k,r | k9, r2, krkr >
k=(abcdefghi) r=(bi)(ch)(dg)(ef) 		1.29.32.96
1
C9

"(C9⋊)⋊C2" / D18 = C3
1, D18
C9
(C3 × C3) ⋊ C2
with the C2 acting separately on the two C3s 		< r,g,b | r2, g2, b2, (rg)3, (rb)3, (gb)3, (rgb)2 >

< r,g,b | r2, g2, b2, (rg)3, (gb)3, (br)3, (rgb)2, (rbg)2, (rgrb)3 >

1.29.38
1
C3×C3

"((C32⋊Q8)⋊C3)⋊C2" / C32⋊C2 = ?
4, (C3 x C3) : C2
C32
19 Abelian C19 < k | k19 >
k=(abcdefghijklmnopqrs) 		1.1918
C19
1

C18 / 1 = C18
1, C19
20 Abelian C20
= C5 × C4 		< k | k20 >
k=(abcdefghijklmnopqrst)

< k,r | k5, r4, krk-1r-1 >
k=(abcde) r=(mnop)

1.2.42.54.104.204
C20
1

C4×C2 / 1 = C4×C2
2, C20
C4
C10 × C2
= C5 × C2 × C2 		< k,r | k10, r2, krk-1r-1 >
k=(abcdefghij) r=(mn)

< r,g,b | r2, gr2, bk5, all commute >

1.2.42.54.1012
C10×C2
1

D6×C4 / 1 = D6×C4
5, C10 x C2
C22
Other direct products D20
= C10 ⋊ C2
≅ D10 × C2 		< k,r | k10, r2, krkr >
k=(abcdefghij) r=(bj)(ci)(dh)(eg)

< r,g,b | r2, g2, b2, (rg)2, b central >

1.21+10.54.104
C2
C5

"C2 x (C5 : C4)" / D10 = ?
4, D20
C22
Other Dic20
≅ C5 ⋊C2 C4 		< k,r | k10, r4, k5r2 >
k=(abcde)(pr)(qs) r=(be)(cd)(pqrs)

< k,r | k5, r4, krkrrr >

1.2.410.54.104
C2
C5

C2×(C5⋊C2C4) / D10 = C2
1, C5 : C4
C4
Frob20
≅ C5 ⋊C4 C4 		< k,g | k4, r2, (rk)4, (rk2)5 > 1.25.410.54
1
C5

C5⋊C4C4 / C5⋊C4C4 = 1
3, C5 : C4
C4
21 Abelian C21
= C7 × C3 		< k | k21 >
k=(abcdefghijklmnopqrstu)

< k,r | k7, r3, krk-1r-1 >
k=(abcdefg) r=(pqr)

1.32.76.2112
C21
1

C6×C2 / 1 = C6×C2
2, C21
Other C7 ⋊ C3 < k,r | k3, r3, (kr)7 >

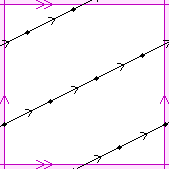
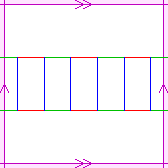
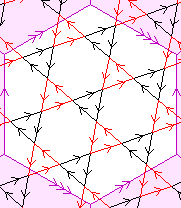
The sides of the triangle formed by the horizontal, the vertical, and the steepest lines in the diagram are in the ratio:
1 : 3*sqrt(3) : 2*sqrt(7).

1.314.76
1
C7
22 Abelian C22
= C11 × C2 		< k | k22 >
k=(abcdefghijklmnopqrstuv)

< k,r | k11, r2, krk-1r-1 >
k=(abcdefghijk) r=(pq)

1.2.1110.2210
C22
1

C10 / 1 = C10
2, C22
Other D22
= C11 ⋊ C2 		< k,r | k11, r2, krkr >
k=(abcdefghijk) r=(bk)(cj()di)(eh)(fg) 		1.211.1110
1
C11

"(C11 : C5) : C2" / D22 = C5
1, D22
23 Abelian C23 < k | k23 >
k=(abcdefghijklmnopqrstuvw) 		1.2322
C23
1

C22 / 1 = C22
1, C23
24 Abelian C24
= C8 × C3 		< k | k24 >
k=(abcdefghijklmnopqrstuvwv)

< k,r | k8, r3, krk-1r-1 >
k=(abcdefgh) r=(mn)

1.2.32.42.62.84.126.246
C24
1

C232 / 1 = C232
2, C24
C8
C12 × C2
= C6 × C4
= C4 × C3 × C2 		< k,r | k12, r2, krk-1r-1 >
k=(abcdefghijkl) r=(pq)

< k,r | k6, r4, krk-1r-1 >
k=(abcdef) r=(pqrs)

1.23.32.44.66.128
C12×C2
1

D8×C2 / 1 = D8×C2
9, C12 x C2
C4×C2
C3 × C2 × C2 × C2
= C6 × C2 × C2
= C2 × C2 × C2 × C3 		< r,g,b | r2, g2, 66, all commute > 1.27.32.614
C3×C2×C2×C2
1

PSL(3,2)×C2 / 1 = PSL(3,2)×C2
15, C6 x C2 x C2
C23
Other direct products D12 × C2
= D6 × C2 × C2 		< r,g,b | r2, g2, b2, (rg)6, b central > 1.215.32.66
C2×C2
C3

S4×D6 / D6 = S4
14, C2 x C2 x S3
C23
D8 × C3 < r,g,b | r2, g2, b3, (rg)4, b central > 1.25.32.42.610.124
C3×C2
C2

D8×C2 / C22 = ?
10, C3 x D8
D8
D6 × C4 < r,g,b | r2, g2, b4, (rg)3, b central > 1.27.32.48.62.124
C4
C3

S3×C22 / S3 = ?
5, C4 x S3
C4×C2
Dic12 × C2
≅ C6 ⋊C2 C4 		< b,r,g | b6, r4, g2, brbbbr, gbgb-1, grgr-1 >
b=(abc)(mo)(np) r=(bc)(mnop) g=(st)

< k,r | k6, r4, krkr3 >
k=(abcdef) r=(bf)(ce)(pqrs)

1.21+2.32.412.66
C22
C3

D8×D6 / D6 = ?
7, C2 x (C3 : C4)
C4×C2
Q8 × C3 < r,b,g | r4, b4, g2, rrbb, rgr-1g-1, bgb-1g-1 > 1.2.32.48.62.1212
C3×C2
C2

S4×C2 / C22 = ?
11, C3 x Q8
Q8
A4 × C2 ≅ (C2×C2×C2) ⋊ C3 < k,r | k6, r2, (k3r)2 >
k3 is central

< k,r | k3, r2, (kr)6 >
(kr)3 is central

1.27.38.68
C2
C2×C2

S4 / A4 = C2
13, C2 x A4
C23
Other D24
= C12 ⋊ C2 		< k,r | k12, r2, krkr>
k=(abcdefghijkl) r=(bl)(ck)(dj)(ei)(fh) 		1.21+12.32.42.62.124
C2
C6

D8×C3 / D12 = C2
6, D24
D8
Dic24

< k,r | k12, r4, k6r2 >
k=(abcdefghijkl)(mnopqrstuvwx) r=(asgm)(brhx)(cqiw)(dpjv)(eoku)(fnlt)

1.2.32.42+12.62.124
C2
C6

D8×C3 / D12 = C2
4, C3 : Q8
Q8
C3 ⋊ C8 < k,r | k8, r3, krk7r >
k=(abc) r=(bc)(defghijk) 		1.2.32.42.62.812.124
C4
C3

D6×C22 / S3 = D6×C22
1, C3 : C8
C8
SL(2,3)
≅ Q8 ⋊ C3 		< k,r | k3, r3, (kr)3 >
k=(abcdef)(gh) r=(gahd)(ecbf)

< r,b,g,e | r4, b4, g4, e3, rrbb, bbgg, ggrr, rbgrbg, rebege>

1.2.38.46.68
C2
Q8

S4 / A4 = C2
3, SL(2,3)
Q8
C3 ⋊ D8
 < k,r,g | k3, g2, r2, (rg)4, (rk)2, (gk)2 >
k=(abc) g=(ghij)(bc) r=(hj)		 1.21+2+6.32.46.66
C2
C6

D6×C22 / D12 = C2
8, (C6 x C2) : C2
D8
S4
≅ (C2×C2) ⋊ D6 		< r,g,b | r2, g2, b2, (rg)3, (gb)3, (br)3, (rgb)4, (rbg)4, (rgrb)2 > 1.23+6.38.46
1
A4

S4 / S4 = 1
12, S4
D8
25 Abelian C25 < k | k25 >
k=(abcdefghijklmnopqrstuvwxy) 		1.54.2520
C25
1

C20 / 1 = C20
1, C25
C5 × C5 < k,r | k5, r5, krk-1r-1>
k=(abcde) r=(fghij) 		1.524
C5×C5
1

GL(2,5) / 1 = GL(2,5)
2, C5 x C5
1
26 Abelian C26
= C13 × C2 		< k | k26 >
k=(abcdefghijklmnopqrstuvwxyz)

< k,r | k13, r2, krk-1r-1 >
k=(abcdefghijklm) r=(pq)

1.2.1312.2612
C26
1

C12 / 1 = C12
2, C26
Other D26
= C13 ⋊ C2 		< k,r | k11, r2, krkr >
k=(abcdefghijklm) r=(bm)(cl)(dk)(ej)(fi)(gh) 		1.213.1312
1
C13

"(C13 : C4) : C3" / D26 = C6
1, D26
27 Abelian C27 < k | k27 >
k=(abcdefghijklmnopqrstuvwxyzæ)

1.32.96.2718
C27
1

C18 / 1 = C18
1, C27
C9 × C3 < k,r | k9, r3, krk-1r-1 >
k=(abcdefghi) r=(pqr)

1.38.918
C9×C3
1

"C2 x (((C3 x C3) : C3) : C2)" / 1 = ?
2, C9 x C3
C3 × C3 × C3 < k,r,g | k3, r3, g3, krk-1r-1, rgr-1g-1, gkg-1g-1 >
k=(abc) r=(def) g=(ghi)

1.327
C33
1

Gl(3,3) / 1 = GL(3,3)
5, C3 x C3 x C3
Other C9 ⋊ C3 < k,r | k9, r3, krk5r-1 >
k=(abcdefghi) r=(beh)(cif) 		1.32+6.918
C3
C3

"((C3 x C3) : C3) : C2" / C32 = ?
4, C9 : C3
(C3 × C3) ⋊ C3 < k,r | k3, r3, (kr)3, (kr2)3 >

1.32+24
C3
C3

"(((C3 x C3) : Q8) : C3) : C2" / C32 = ?
3, (C3 x C3) : C3
28 Abelian C28
= C7 × C4 		< k | k28 >
k=(abcdefghijklmnopqrstuvwxyzæð)

< k,r | k7, r4, krk-1r-1 >
k=(abcdefg) r=(mnop)

1.2.42.76.2118
C28
1

C6×C2 / 1 = C6×C2
2, C28
C4
C14 × C2
= C7 × C2 × C2 		< k,r | k14, r2, krk-1r-1 >
k=(abcdefg) r=(pq)

< r,g,b | k2, g2, bk7, all comute >

1.23.76.1418
C14×C2
1

D6×C6 / 1 = D6×C6
4, C14 x C2
C22
Other direct products D28
= C14 ⋊ C2
≅ D14 × C2 		< k,r | k14, r2, krkr >
k=(abcdefghijklmn) r=(bn)(cm)(dl)(ek)(fj)(gj)

< r,g,b | r2, g2, b2, (rg)b7, b central >

1.21+2+12.76.146
C2
C7

(C7⋊C6)×C2 / D14 = C6
3, D28
C22
Other Dic28
≅ C7 ⋊C2 C4 		< k,r | k14, r4, k7r2 >
k=(abcdefg)(pr)(qs) r=(bg)(cf)(de)(pqrs) 		1.2.414.76.146
C2
C7

(C7⋊C6)×C2 / D14 = C6
1, C7 : C4
C4
29 Abelian C29 < k | k29 >
k=(abcdefghijklmnopqrstuvwxyzæðñ) 		1.2928
C29
1

C28 / 1 = C28
1, C29
30 Abelian C30
= C15 × C2
= C10 × C3
= C6 × C5
= C5 × C3 × C2
 < k | k30 >
k=(abcdefghijklmnopqrstuvwxyzæðñç)

< k,r | k15, r2, krk-1r-1 >
k=(abcdefghijklmno) r=(pq)

< k,r | k10, r3, krk-1r-1 >
k=(abcdefghij) r=(klm)

< k,r | k6, r5, krk-1r-1 >
k=(abcdef) r=(ghijk)

1.2.32.54.62.104.158.308
C30
1

C4×C2 / 1 = C4×C2
4, C30
Other direct products D10 × C3 < r,g,b | r2, g2, b3, (rg)5, b central > 1.25.32.54.610.158
C3
C5

(C5⋊C4)×C2 / D10 = C22
2, C3 x D10
D6 × C5 < r,g,b | r2, g2, b5, (rg)3, b central > 1.23.32.54.1012.158
C5
C3

D6×C4 / D6 = C4
1, C5 x S3
Other D30
C15 ⋊ C2 		< k,r | k15, r2, abab >
k=(abcdefghijklmno) r=(bo)(cn)(dm)(el)(fk)(gj)(hi) 		1.215.32.54.158
1
C15

(C5⋊C4)×D6 / D6 = ?
3, D30
31 Abelian C31 < k | k31 >
k=(abcdefghijklmnopqrstuvwxyzæðñçþ) 		1.3130
C31
1

C30 / 1 = C30
1, C31

Other pages giving Cayley diagrams of groups with fewer than 32 elements:

Some more Cayley diagrams
Some more pages on groups

Copyright N.S.Wedd 2009