This page gives Cayley diagrams for all groups of order less than 32
which are not direct products.
Their presentations are also given.
The letters in the presentations correspond to the colours in the Cayley diagrams:
black
red
green
blue
mauve
grey.
Some of the notation used here is non-standard. If you want a page that uses
standard notation, and has no little orange triangles indicating central extensions,
see Cayley Diagrams of Small Groups.
An integer denotes the cyclic group of that order — the letter "C" (or "Z")
indicating a cyclic group is omitted. Composite integers are not used.
The orange triangles in the Cayley diagrams of central extensions are explained in
the page on toll-bean extensions.
| Order |
|
Name |
Presentation
generators as permutations |
Cayley diagram |
Orders of elements.
Centre.
Derived subgroup. |
|
1
|
Abelian
|
1
|
<>
|
 |
1 1 1 |
|
2
|
Abelian
|
2
|
< k | k2 >
k=(ab) |
 |
1.2 2 1 |
|
3
|
Abelian
|
3
|
< k | k3 >
k=(abc)
|
 |
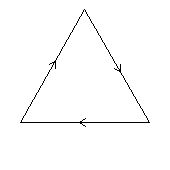1.32 3 1 |
|
4
|
Abelian
|
2×2
|
|
| 1.23 2×2 1 |
|
2↑2
|
< k | k4 >
k=(abcd)
|
 |
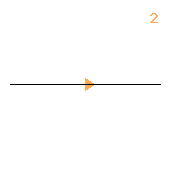1.2.42 2↑2 1 |
|
5
|
Abelian
|
5
|
< k | k5 >
k=(abcde)
|
 |
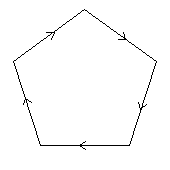1.54 5 1 |
|
6
|
Abelian
|
2×3
|
|
| 1.2.32.62 6 1 |
|
Other
|
3⋊2
|
< k,r | k3, r2, krkr >
k=(abc) r=(bc)
|
 |
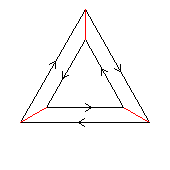1.23.32 1 3 |
|
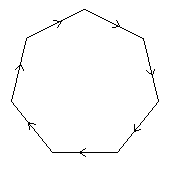
7
|
Abelian
|
7
|
< k | k7 >
k=(abcdefg)
|
 |
1.76 7 1 |
|
8
|
Abelian
|
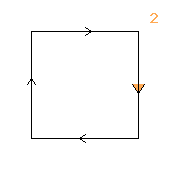
2↑2↑2
|
< k | k8 >
k=(abcdefgh)
|
 |
1.2.42.84 2↑2↑2 1 |
|
(2↑2)×2
|
|
| 1.21+2.44 (2↑2)×2 1 |
|
2×2×2
|
|
| 1.27 2×2×2 1 |
|
Other
|
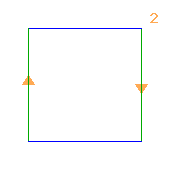
(2↑2)⋊2 |
< k,r | r4, r2, krkr >
k=(abcd) r=(ac)
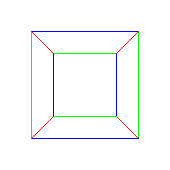
< r,g,b | b2, g2, r2,
bgbg, rbrg, rgrb >
b=(ab)(cd) g=(ac)(bd) r=(bc)
|
| 1.21+4.42 2 2 |
|
2↑(2×2)
|
< k,r | k4, r4, krkkkr, kkrr >
k=(abcd)(efgh) r=(ahcf)(bgde)
|
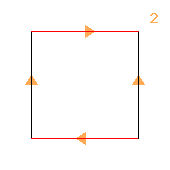
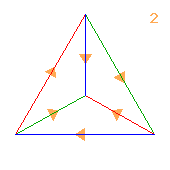
| 1.2.46 2 2 |
|
9
|
Abelian
|
3↑3
|
< k | k9 >
k=(abcdefghi)
|
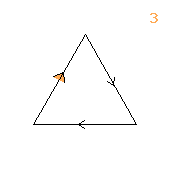
| 1.32.66 3↑3 1 |
|
3×3
|
|
| 1.38 3×3 1 |
|
10
|
Abelian
|
2×5
|
|
| 1.2.54.104 2×5 1 |
|
Other
|
5⋊2
|
< k,r | k5, r2, krkr >
k=(abcde) r=(be)(cd)
|
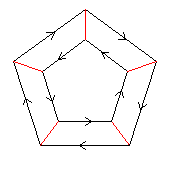
| 1.25.54 1 5 |
|
11
|
Abelian
|
11
|
< k | k11 >
k=(abcdefghijk)
|
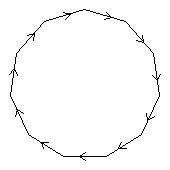
| 1.1110 11 1 |
|
12
|
Abelian
|
(2↑2)×3
|
|
| 1.2.32.42.62.124 (2↑2)×3 1 |
|
2×2×3
|
|
| 1.23.32.66 2×2×3 1 |
|
Other d.p.
|
2×(3⋊2)
|
|
| 1.21+6.32.62 2 3 |
|
Other
|
3⋊(2↑2)
|
< b,r | b6, r4, rkrrrk >
b=(abc)(pr)(qs) r=(bc)(pqrs)
|
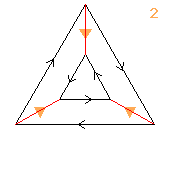
| 1.2.32.46.62 2 3 |
|
(2×2)⋊3
(a.k.a. A4)
|
< k,r | k3, r2, (kr)3 >
k=(abc) r=(ab)(cd)
|
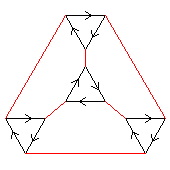
| 1.23.38 1 2×2 |
|
13
|
Abelian
|
13
|
< k | k13 >
k=(abcdefghijklm)
|
| 1.1312 13 1 |
|
14
|
Abelian
|
2×7
|
|
| 1.2.76.146 2×7 1 |
|
Other
|
7⋊2
|
< k,r | k7, r2, krkr >
k=(abcdefg) r=(bg)(cf)(de)
|
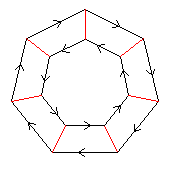
| 1.27.76 1 7 |
|
15
|
Abelian
|
3×5
|
|
| 1.32.54.158 3×5 1 |
|
16
|
Abelian
|
2↑2↑2↑2
|
< k | k16 >
k=(abcdefghijklmnop)
|
| 1.2.42.84.168 2↑2↑2↑2 1 |
|
2×(2↑2↑2)
|
|
| 1.23.44.88 2×(2↑2↑2) 1 |
|
(2↑2)×(2↑2)
|
|
| 1.23.412 (2↑2)×(2↑2) 1 |
|
2×2×(2↑2)
|
|
| 1.21+6.48 2×2×(2↑2) 1 |
|
2×2×2×2
|
|
| 1.215 2×2×2×2 1 |
|
Other d.p.s
|
2×((2↑2)⋊2)
|
|
| 1.21+2+8.44 2×2 2 |
|
2×(2↑(2×2))
|
|
| 1.21+2.412 2×2 2 |
|
Other
|
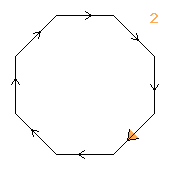
(2↑2↑2)⋊2
(dihedral)
|
< k,r | k8, r2, krkr >
k=(abcdefgh) r=(bh)(cg)(df)
|
| 1.21+8.42.84 2 2↑2 |
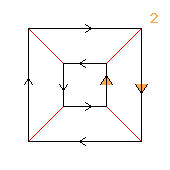
(2↑2↑2)⋊2
≅ (2↑2)↑(2×2)
(modular)
|
< k,r | k8, r2, krkkkr >
k=(abcdefgh) r=(bf)(dh)
|
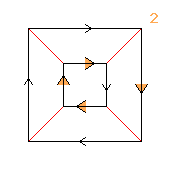
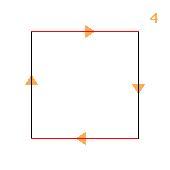
| 1.21+2.44.88 2↑2 2 |
|
(2↑2↑2)⋊2
(quasidihedral, semidihedral)
|
< k,r | k8, r2, krkkkkkr >
k=(abcdefgh) r=(bd)(cg)(fh)
|
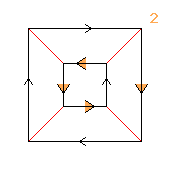
| 1.21+4.46.84 2 2↑2 |
|
2↑((2↑2)⋊2)
(Q16)
|
< k,r | k8, r4, (kr)4, rkr3k >
k=(abcdefgh)(pqrstuvw) r=(apet)(bwfs)(cvgr)(duhq)
|
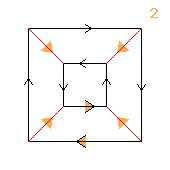
| 1.2.410.84 2 2↑2 |
|
(2↑2)⋊(2↑2)
≅ 2↑(2×2×2)
|
< k,r | k4, r4, krkr3 >
k=(abcd) r=(bd)(efgh)
< b,g,r | b4, g4, r4, (bgr)2 >
|
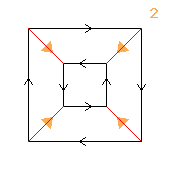
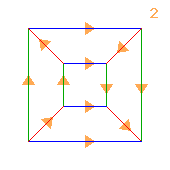
| 1.23.412 2×2 2 |
|
(2×2)⋊(2↑2)
|
< b,g,r | b2, g2, r4, bgbg, rbrrrg, rgrrrb >
b=(ab)(cd) g=(ac)(bd) r=(bc)(pqrs)
|
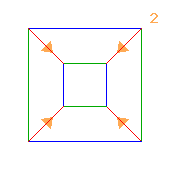
| 1.23+4.48 2×2 2 |
((2↑2)⋊2)⋊2
≅ (2↑(2×2))⋊2
≅ ((2↑2)×2)⋊2
≅ ((2↑2)↑(2×2)
Pauli
|
< r,g,b | r2, g4, b4, (rg)2, (gb)4, (br)4 >
r=(bd)(eg) g=(agce)(bfdh) b=(afch)(bedg)
r and g generate (2↑2)⋊2; g and b generate 2↑(2×2); b and r generate (2↑2)×2.
Thus, if we regard the Cayley diagram as a cube, two opposite faces portray D8, two others Q8, and the other two C4×C2.
(br) generates the centre.
|
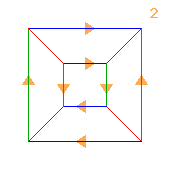
| 1.21+2+2+2.42+6 2↑2 2 |
|
17
|
Abelian
|
17
|
< k | k17 >
k=(abcdefghijklmnopq)
|
| 1.1716 17 1 |
|
18
|
Abelian
|
2×(3↑3)
|
|
| 1.2.32.62.96.186 2×(3↑3) 1 |
|
2×3×3
|
|
| 1.2.38.68 2×3×3 1 |
|
Other d.p.
|
3×(3⋊2)
≅ (3×3)⋊2
|
with the 2 interchanging the generators of the 3s
|
| 1.23.38.66 C3 C3 |
|
Other
|
(3↑3)⋊2
|
< k,r | k9, r2, krkr >
k=(abcdefghi) r=(bi)(ch)(dg)(ef)
|
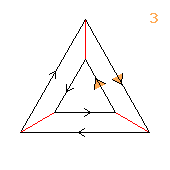
| 1.29.32.96 1 3↑3 |
(3×3)⋊2
with the 2 acting separately on the two 3s.
|
< k,r,g | k3, r3, c2, krkkrr, kgkg, rgrgr >
k=(abc) r=(def) g=(bc)(ef)
|
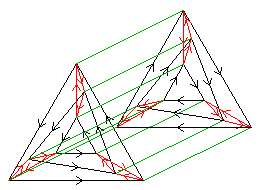
| 1.29.38 1 3×3 |
|
19
|
Abelian
|
19
|
< k | k19 >
k=(abcdefghijklmnopqrs)
|
| 1.1918 19 1 |
|
20
|
Abelian
|
(2↑2)×5
|
|
| 1.2.42.54.104.204 (2↑2)×5 1 |
|
2×2×5
|
|
| 1.2.42.54.1012 2×2×5 1 |
|
Other d.p.
|
2×(5⋊2)
|
|
| 1.21+10.54.104 2 5 |
|
Other
|
5⋊2(2↑2)
|
< k,r | k5, r4, krkrrr >
b=(abcde)(pr)(qs) r=(be)(cd)(pqrs)
|
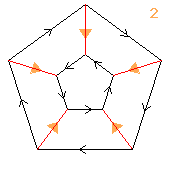
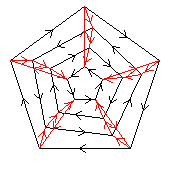
| 1.2.410.54.104 2 5 |
|
5⋊2↑2(2↑2)
|
< k,g | k5, g4, kgkkggg >
k=(abcde) g=(bced)
|
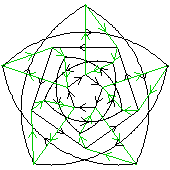
| 1.25.410.54 1 5 |
|
21
|
Abelian
|
3×7
|
|
| 1.32.76.2112 3×7 1 |
|
Other
|
7⋊3
|
< k,r | k7, r3, krk5r2 >
k=(abcdefg) r=(bce)(dgf)
|
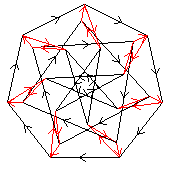
| 1.314.76 1 7 |
|
22
|
Abelian
|
2×11
|
|
| 1.2.1110.2210 2×11 1 |
|
Other
|
11⋊2
|
< k,r | k11, r2, krkr >
k=(abcdefghijk) r=(bk)(cj()di)(eh)(fg)
|
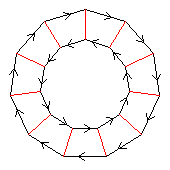
| 1.211.1110 1 11 |
|
23
|
Abelian
|
23
|
< k | k23 >
k=(abcdefghijklmnopqrstuvw)
|
| 1.2322 23 1 |
|
24
|
Abelian
|
(2↑2↑2)×3
|
|
| 1.2.32.42.62.84.126.246 (2↑2↑2)×3 1 |
|
2×(2↑2)×3
|
|
| 1.23.32.44.66.128 2×(2↑2)×3 1 |
|
2×2×2×3
|
|
| 1.27.32.614 2×2×2×3 1 |
|
Other d.p.s
|
2×2×(3⋊2)
|
|
| 1.215.32.66 2×2 3 |
|
3×((2↑2)⋊2)
|
|
| 1.25.32.42.610.124 2×3 2 |
|
(2↑2)×(3⋊2)
|
|
| 1.27.32.48.62.124 2↑2 3 |
|
2×(3⋊(2↑2))
|
|
| 1.21+2.32.412.66 2×2 3 |
|
3×(2↑(2×2))
|
|
| 1.2.32.48.62.1212 2×3 2 |
|
2×((2×2)⋊3)
|
|
| 1.27.38.68 2 2×2 |
|
Other
|
((2↑2)×3)⋊2)
|
< k,r | k12, r2, krkr>
k=(abcdefghijkl) r=(bl)(ck)(dj)(ei)(fh)
|
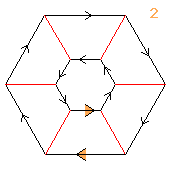
| 1.21+12.32.42.62.124 2 6 |
|
2↑(2×(3⋊2))
|
< k,r | k12, r4, krkrrr >
b=(abcdefghijkl)(mnopqrstuvwx) r=(asgm)(brhx)(cqiw)(dpjv)(eoku)(fnlt)
|
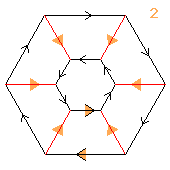
| 1.2.32.42+12.62.124 2 6 |
|
3⋊(2↑2↑2)
|
< k,r | k3, r8, krkr7 >
k=(abc) r=(bc)(defghijk)
|
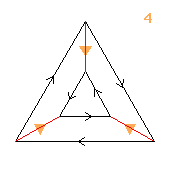
| 1.2.32.42.62.812.124 2↑2 3 |
|
3⋊((2↑2)⋊2)
|
< k,r,g | k3, g4, r2,
gkgggk, rgrg, rkr-1k-1 >
k=(abc) g=(ghij)(bc) r=(hj)
|
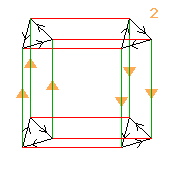
| 1.21+2+6.32.46.66 2 2×3 |
(2↑(2×2))⋊3
≅ 2↑((2×2))⋊3)
a.k.a. SL(2,3)
|
< k,r | k3, r4, (kr)3 >
k=(abc) r=(ab)(cd)(pq)
< r,b,g,e | r4, b4, g4, e3,
rrbb, bbgg, ggrr, rbgrbg, rebege>
|
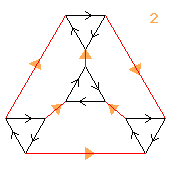
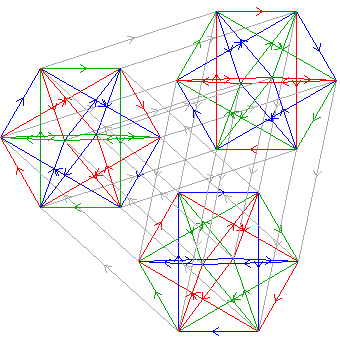
| 1.2.38.46.68 2 2↑(2×2) |
(2×2)⋊(3⋊2)
≅ ((2×2)⋊3)⋊2
a.k.a. S4
|
< k,r | k4, r2, (kr)3 >
k=(abcd) r=(ab)
< k,r | k3, r2, (kr)4 >
k=(abc) r=(cd)
|
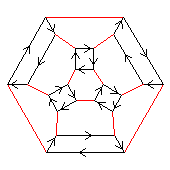
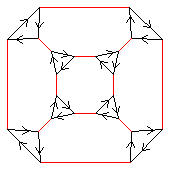
| 1.23+6.38.46 1 (2×2)⋊3 |
|
25
|
Abelian
|
5↑5
|
< k | k25 >
k=(abcdefghijklmnopqrstuvwxy)
|
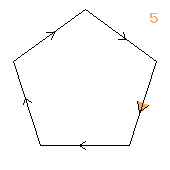
| 1.54.2520 5↑5 1 |
|
5×5
|
|
| 1.524 5×5 1 |
|
26
|
Abelian
|
2×13
|
|
| 1.2.1312.2612 2×13 1 |
|
Other
|
13⋊2
|
< k,r | k11, r2, krkr >
k=(abcdefghijklm) r=(bm)(cl)(dk)(ej)(fi)(gh)
|
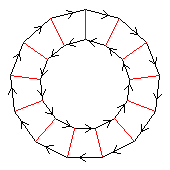
| 1.213.1312 1 13 |
|
27
|
Abelian
|
3↑3↑3
|
< k | k27 >
k=(abcdefghijklmnopqrstuvwxyzæ)
|
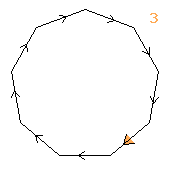
| 1.32.96.2718 3↑3↑3 1 |
|
3×(3↑3)
|
|
| 1.32+6.918 3×(3↑3) 1 |
|
3×3×3
|
|
| 1.327 3×3×3 1 |
|
Other
|
(3↑3)⋊3
|
< k,r | k9, r3,
rkr2k5 >
k=(abcdefghi) r=(bhe)(cfi)
|
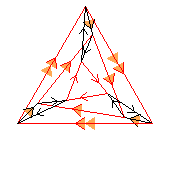
| 1.32+6.918 3 3 |
|
(3×3)⋊3
|
< k,r | k3, r3, (k,r)3 >
k=(abc)(def)(ghi) r=(adg)(bhe)
|
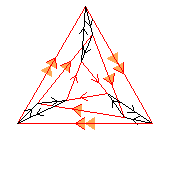
| 1.32+24 3 3 |
|
28
|
Abelian
|
(2↑2)×7
|
|
| 1.2.42.76.2118 (2↑2)×7 1 |
|
2×2×7
|
|
| 1.23.76.1418 2×2×7 1 |
|
Other d.p.
|
2×(7⋊2)
|
|
| 1.21+2+12.76.146 2 7 |
|
Other
|
7⋊(2↑2)
|
< b,r | b7, r4, brbrrr >
b=(abcdefg)(pr)(qs) r=(bg)(cf)(de)(pqrs)
|
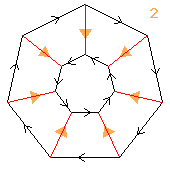
| 1.2.414.76.146 2 7 |
|
29
|
Abelian
|
29
|
< k | k29 >
k=(abcdefghijklmnopqrstuvwxyzæðñ)
|
| 1.2928 29 1 |
|
30
|
Abelian
|
2×3×5
|
|
| 1.2.32.54.62.104.158.308 2×3×5 1 |
|
Other d.p.s
|
3×(5⋊2)
|
|
| 1.25.32.54.610.158 3 5 |
|
5×(3⋊2)
|
|
| 1.23.32.54.1012.158 5 3 |
|
Other
|
(3×5)⋊2
|
< k,r | k15, r2, abab >
k=(abcdefghijklmno) r=(bo)(cn)(dm)(el)(fk)(gj)(hi)
|
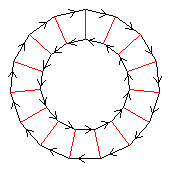
| 1.215.32.54.158 1 3×5 |
|
31
|
Abelian
|
31
|
< k | k31 >
k=(abcdefghijklmnopqrstuvwxyzæðñçþ)
|
| 1.3130 31 1 |