Double Cayley Diagrams of Small Groups

This page shows double Cayley diagrams of some small groups. A double Cayley diagram for a group G is two Cayley diagrams shown together. One (in dark colours) is the Cayley diagram of G, and looks similar to the Cayley diagram of G given at Cayley Diagrams of Small Groups. The other (in light colours) is a Cayley diagram of its automorphism group aut(G), using the same set of points.

The identity of G is fixed under all the automorphisms, and is shown by a black blob.

The last diagram for C16 is the most pleasing.

GroupAutomorphism groupCayley diagram
{1} {1}
C2 {1}
C3 C2
C4 C2
C2×C2 D6
C5 C4
C6 C2
D6 D6
C7 C6
C8 C2×C2
C4×C2 D8

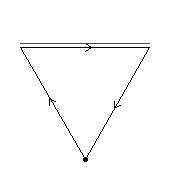
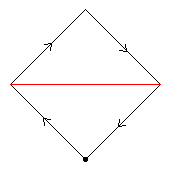
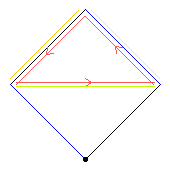
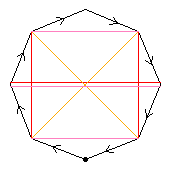
If the C4 is < a,b | a4=1=b2, ab=ba >,
then a 4-cycle of the D8 is generated by the permutation (a ab a3 a3b)(b a2b)
and the mirrors are (a b)(a3 a3b), (a a3b)(a3 ab), (ab a3b)(b a2b), and (a a3)(b a2b).

C2×C2×C2 GL(3,2) ≅ PSL(2,7), the simple group of order 168. no diagram
D8 D8

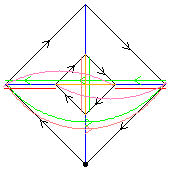
The automorphisms, as shown in the diagram, are exactly the same as for C4×C2 above. Only the underlying group is different.

Q8 D6 no diagram
C9 C6
C3×C3 GL(2,3) no diagram
C10 C4
D10 The Frobenius group of order 20 no diagram
C11 C10
C12 C2×C2
C6×C2 D6 no diagram
D12 D12 no diagram
A4 S4 no diagram
Dic12 D12 no diagram
C13 C12
C14 C6
D14 D14 no diagram
C15 C4×C2

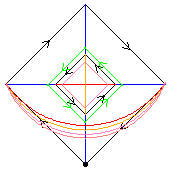
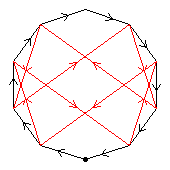
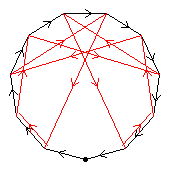
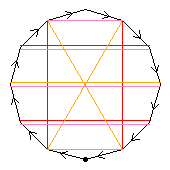
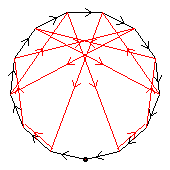
From here on, only very few groups will be listed

C16 C4×C2

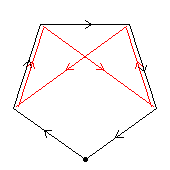
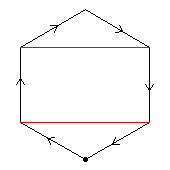
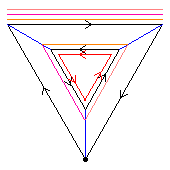
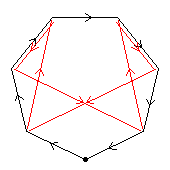
The first diagram, green, shows one of the C2 automorphisms. If we apply this automorphism to build C4⋊C2, we get D32.

The second diagram, red, shows another C2 automorphism. If we apply this automorphism to build C4⋊C2, we get the modular group of order 32.

The third diagram, blue, shows a C4 automorphism. The dark blue shows an automorphism of order 4; the pale blue, the square of this automorphism. If we apply the pale blue automorphism to build C4⋊C2, we get the quasidihedral group of order 32.

The fourth diagram shows all three order-2 automorphisms, together forming C2×C2.

C17 C16

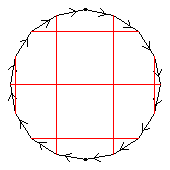
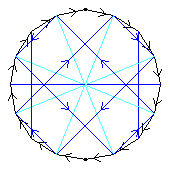
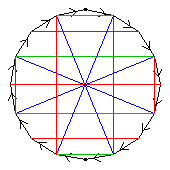
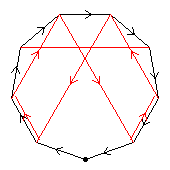
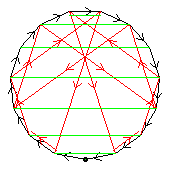
The C17 itself is not shown, for the sake of clarity; it is of course the surrounding 17-gon. For aut(C17), only the elements of period 16 are shown, and the arrows are omitted.

There are many more diagrams like this at the page Double Cayley Diagrams of Small Groups of Prime Order.


For some more double Cayley diagrams, see Double Cayley Diagrams of Small Groups of Prime Order.

C32 C8×C2

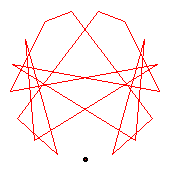
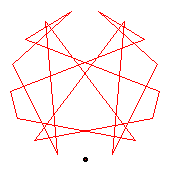
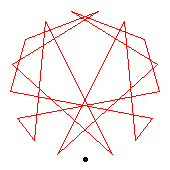
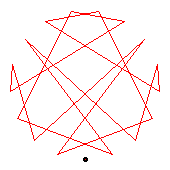
The first two diagrams show two of the C2 automorphisms.

The third diagram shows a C8 automorphism. The dark blue shows an automorphism of order 8; the pale blue, the fourth power of this automorphism.

The fourth diagram shows all three order-2 automorphisms, together forming C2×C2.

C64 C16×C2

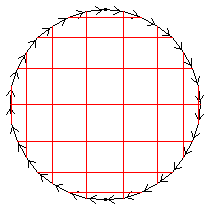
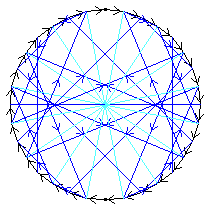
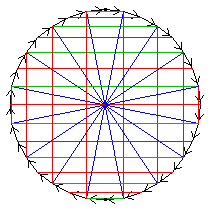
The first two diagrams show two of the C2 automorphisms.

The third diagram, blue, shows a C16 automorphism. The dark blue shows an automorphism of order 16; the arrows have been omitted from the dark blue lines, for the sake of clarity. The pale blue shows the eighth power of this automorphism.

The fourth diagram shows all three order-2 automorphisms, together forming C2×C2.

C128 C32×C2

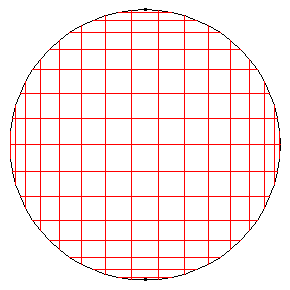
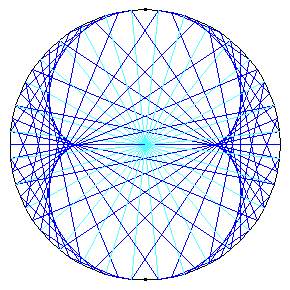
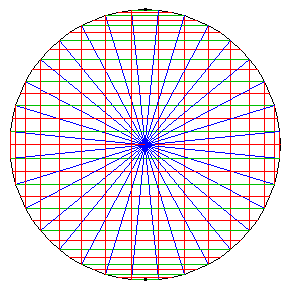
The first two diagrams show two of the C2 automorphisms.

The third diagram, blue, shows a C32 automorphism. The dark blue shows an automorphism of order 32; the arrows have been omitted from the dark blue lines, for the sake of clarity. The pale blue shows the sixteenth power of this automorphism.

The fourth diagram shows all three order-2 automorphisms, together forming C2×C2.

Click on any of these four diagrams to see a larger version.
C256 C64×C2

The first two diagrams show two of the C2 automorphisms.

The third diagram, blue, shows a C64 automorphism. The dark blue shows an automorphism of order 64; the arrows have been omitted from the dark blue lines, for the sake of clarity. The pale blue shows the 32nd power of this automorphism.

The fourth diagram shows all three order-2 automorphisms, together forming C2×C2.

Click on any of these four diagrams to see a larger version.

Some larger double Cayley diagrams
Some more Cayley diagrams
and other pages on groups
Copyright N.S.Wedd 2007