Double Cayley Diagrams of Small Groups of Prime Order

This page shows double Cayley diagrams of small groups of prime order, up to order 149. Double Cayley diagrams are described, and some shown, in the page Double Cayley Diagrams of Small Groups.

For the ones on this page, the arcs (shown in black on that page) for the group of prime order itself are omitted for the sake of clarity. It is obvious where they belong, they form a regular p-gon. The red arcs are Cayley diagrams for the automorphism group of the group of prime order. The identity of the group of prime order is shown as a black dot.

For any prime p, the automorphism group of Cp is C(p-1), which has elements of all orders dividing p-1. This page shows all, and only, those automorphisms which have order p-1. For example, if C11 is regarded as the integers modulo 11 under addition, the automorphisms are the results of multiplication by 2, 6, 7 or 8 modulo 11, being four 10-cycles. 2 and 6, and 7 and 8, give the same 10-cycles traversed in opposite directions. No maximum-cycle generator can be a quadratic residue of the prime.

Some of the more pleasing diagrams are

3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | 29 | 31 | 37 | 41 | 43 | 47 | 53 | 59 | 67 | 71 | 79 | 79 | 83 | 89 | 97 | 101 | 103 | 107 | 109 | 113 | 127 | 131 | 137 | 139 | 149

GroupAutomorphism groupCayley diagram
C2 {1}
C3 C2

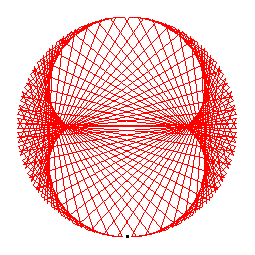
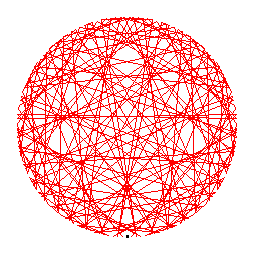
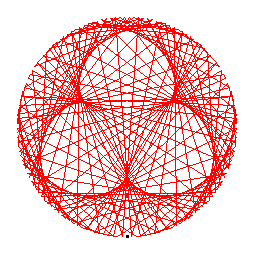
The generator of the 2-cycle is 2.

C5 C4

The generators of the 4-cycle are 2(3).

C7 C6

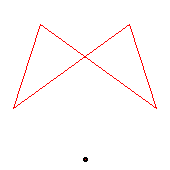
The generators of the 6-cycle are 3(5).

C11 C10

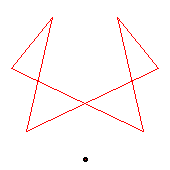
The generators of the 10-cycles are 2(6), 7(8).

C13 C12

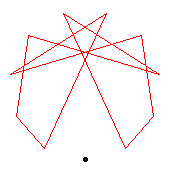
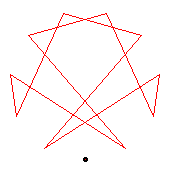
The generators of the 12-cycles are 2(7), 6(11).

C17 C16

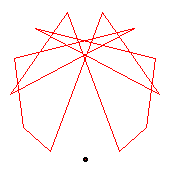
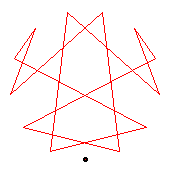
The generators of the 16-cycles are 3(6), 5(7), 10(12), 11(14).

C19 C18

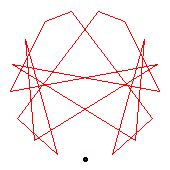
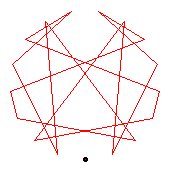
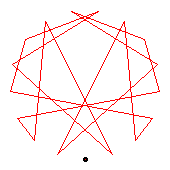
The generators of the 18-cycles are 2(10), 3(13), 14(15).

C23 C22

The generators of the 22-cycles are 5(14), 7(10), 11(21), 15(20), 17(19).

C29 C28

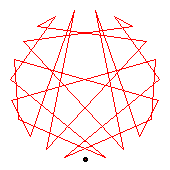
The generators of the 28-cycles are 2(15), 3(10), 8(11), 14(27), 18(21), 19(26).

C31 C30

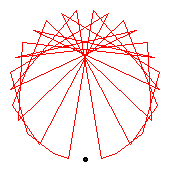
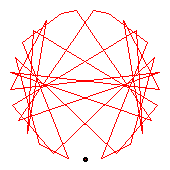
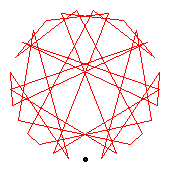
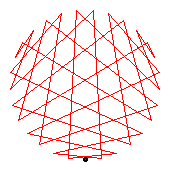
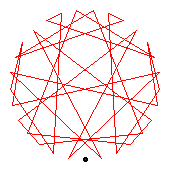
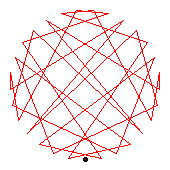
The generators of the 30-cycles are 3(21), 11(17), 12(13), 22(24).

C37 C36

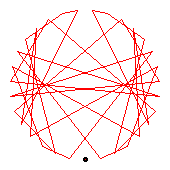
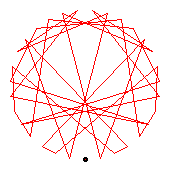
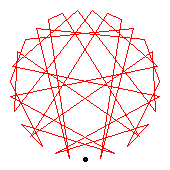
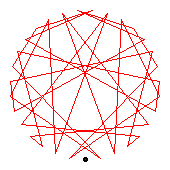
The generators of the 36-cycles are 2(19), 5(15), 13(20), 17(24), 18(35), 22(32).

C41 C40

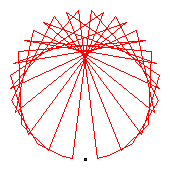
The generators of the 40-cycles are 6(7), 11(15), 12(24), 13(19), 17(29), 22(28), 26(30), 34(35).

C43 C42

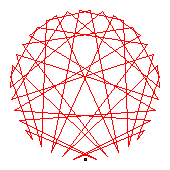
The generators of the 42-cycles are 3(29), 5(26), 12(18), 19(34), 20(28), 30(33).

C47 C46

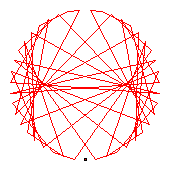
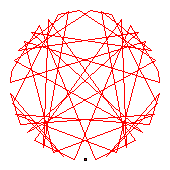
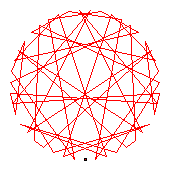
The generators of the 46-cycles are 5(19), 10(33), 11(30), 13(29), 15(22), 20(40), 23(45), 26(38), 31(44), 35(43), 39(41).

C53 C52

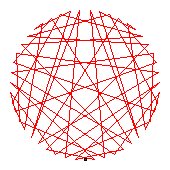
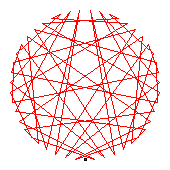
The generators of the 52-cycles are 2(27), 3(18), 5(32), 8(20), 12(31), 14(19), 21(48), 22(41), 26(51), 33(45), 34(39), 35(50).

C59 C58

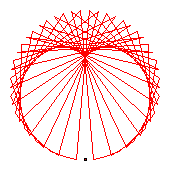
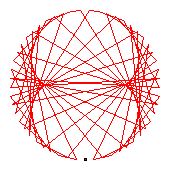
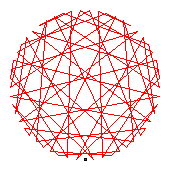
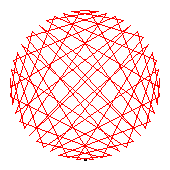
The generators of the 58-cycles are 2(30), 6(10), 8(37), 11(43), 13(50), 14(38), 18(23), 24(32), 31(40), 33(34), 39(56), 42(52), 44(55), 47(54).

C61 C60

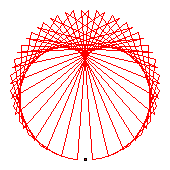
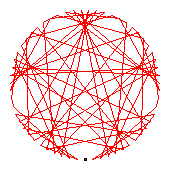
The generators of the 60-cycles are 2(31), 6(51), 7(35), 10(55), 17(18), 26(54), 30(59), 43(44).

C67 C66

The generators of the 66-cycles are 2(34), 7(48), 11(61), 12(28), 13(31), 18(41), 20(57), 32(44), 46(51), 50(63).

C71 C70

The generators of the 70-cycles are 7(61), 11(13), 21(44), 22(42), 28(33), 31(55), 35(69), 47(68), 52(56), 53(67), 59(65), 62(63).

C73 C72

The generators of the 72-cycles are 5(44), 11(20), 13(45), 14(47), 15(39), 26(59), 28(60), 29(68), 31(33), 34(58), 40(42), 53(62).

C79 C78

The generators of the 78-cycles are 3(53), 6(66), 7(34), 28(48), 29(30), 35(70), 37(47), 39(77), 43(68), 54(60), 59(75), 63(74).

C83 C82

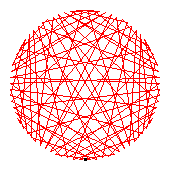
The generators of the 82-cycles are 2(42), 5(50), 6(14), 8(52), 13(32), 15(72), 18(60), 19(35), 20(54), 22(34), 24(45), 39(66), 43(56), 46(74), 47(53), 55(80), 57(67), 58(73), 62(79), 71(76).

C89 C88

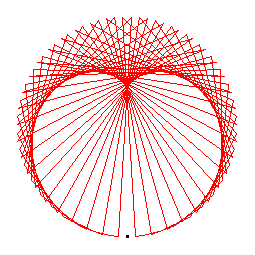
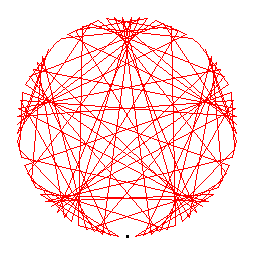
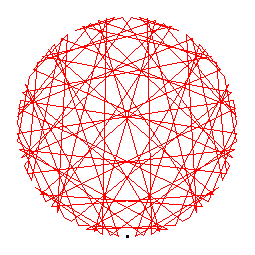
The generators of the 88-cycles are 3(30), 6(15), 7(51), 13(48), 14(70), 19(75), 23(31), 24(26), 27(33), 28(35), 29(43), 38(82), 41(76), 46(60), 54(61), 56(62), 58(66), 59(86), 63(65), 74(83).

C97 C96

The generators of the 96-cycles are 5(39), 7(14), 10(68), 13(15), 17(40), 21(37), 23(38), 26(56), 29(87), 41(71), 57(80), 58(92), 59(74), 60(76), 82(84), 83(90).

C101 C100

The generators of the 100-cycles are 2(51), 3(34), 7(29), 8(38), 11(46), 12(59), 15(27), 18(73), 26(35), 28(83), 40(48), 42(89), 50(99), 53(61), 55(90), 63(93), 66(75), 67(98), 72(94), 74(86).

C103 C102

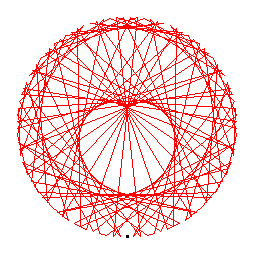
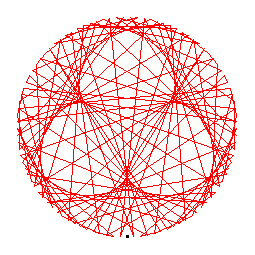
The generators of the 102-cycles are 5(62), 6(86), 11(75), 12(43), 20(67), 21(54), 35(53), 40(85), 44(96), 45(87), 48(88), 51(101), 65(84), 70(78), 71(74), 77(99).

C107 C106

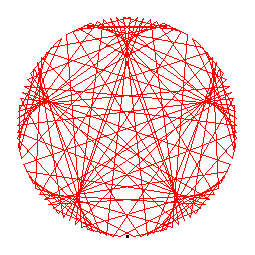
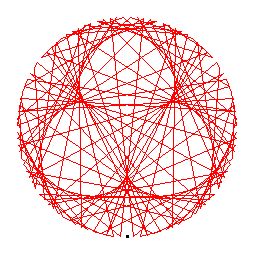
The generators of the 106-cycles are 2(54), 5(43), 6(18), 7(46), 8(67), 15(50), 17(63), 20(91), 21(51), 22(73), 24(58), 26(70), 28(65), 31(38), 32(97), 45(88), 55(72), 59(78), 60(66), 68(96), 71(104), 74(94), 77(82), 80(103), 84(93), 95(98).

C109 C108

The generators of the 108-cycles are 6(91), 10(11), 13(42), 14(39), 18(103), 24(50), 30(40), 37(56), 44(57), 47(58), 51(62), 52(65), 53(72), 59(85), 67(96), 69(79), 70(95), 98(99).

C113 C112

The generators of the 112-cycles are 3(38), 5(68), 6(19), 10(34), 12(66), 17(20), 21(70), 23(59), 24(33), 27(67), 29(39), 37(55), 43(92), 45(108), 46(86), 47(101), 54(90), 58(76), 74(84), 75(110), 79(103), 80(89), 93(96), 94(107).

C127 C126

The generators of the 126-cycles are 3(85), 6(106), 7(109), 12(53), 14(118), 23(116), 29(92), 39(114), 43(65), 45(48), 46(58), 55(97), 56(93), 57(78), 67(91), 83(101), 86(96), 110(112).

C131 C130

The generators of the 130-cycles are 2(66), 6(22), 8(82), 10(118), 14(103), 17(54), 23(57), 26(126), 29(122), 30(83), 31(93), 37(85), 40(95), 50(76), 56(124), 67(88), 72(111), 87(128), 90(115), 96(116), 97(104), 98(127), 106(110), 119(120).

C137 C136

The generators of the 136-cycles are 3(46), 5(55), 6(23), 12(80), 13(116), 20(48), 21(124), 24(40), 26(58), 27(66), 29(52), 31(84), 33(54), 35(47), 42(62), 43(51), 45(67), 53(106), 57(125), 70(92), 71(110), 75(95), 79(111), 82(132), 83(104), 85(108), 86(94), 89(117), 90(102), 91(134), 97(113), 114(131).

C139 C138

The generators of the 138-cycles are 2(70), 3(93), 12(58), 15(102), 17(90), 18(85), 19(22), 21(53), 26(123), 32(126), 40(73), 50(114), 56(72), 61(98), 68(92), 88(109), 101(128), 104(135), 108(130), 110(115), 111(134), 119(132).

C149 C148

The generators of the 148-cycles are 2(75), 3(50), 8(56), 10(15), 11(122), 12(87), 13(23), 14(32), 18(58), 21(71), 27(138), 34(57), 38(51), 40(41), 43(52), 48(59), 55(84), 60(77), 62(137), 65(94), 66(70), 72(89), 74(147), 78(128), 79(83), 90(101), 91(131), 92(115), 93(141), 97(106), 98(111), 99(146), 108(109), 117(135), 126(136), 134(139).

Some smaller double Cayley diagrams
Some more Cayley diagrams
and other pages on groups
Copyright N.S.Wedd 2007