The Genus-2 Regular Map {5,10}

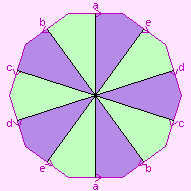
This genus-2 regular map, shown to the right, has two pentagonal faces, each meeting itself five times at the single vertex. It has five edges, and a Euler characteristic of -2.

Its dual is {10,5}. Its double cover is not a regular map [?]. Its Petrie dual is the 5-hemihosohedron.

Its rotational symmetry group is D10.

The face shares all its vertices with itself. The edges join a vertex to itself. Some readers may consider that this invalidates it as a regular map.

Its holes are Eulerian, with ten edges. Its Petrie polygons have two edges.

Antipodal Faces and Vertices

The two faces are antipodal. The five edges form a single antipodal set. Rotating any one edge about its centre causes every other edge to remain where it is and rotate about its own centre: this is the involution of its rotational symmetry group.