The Genus-3 Regular Map {7,3}

This regular map has 24 heptagonal faces, of which three meet at each of its 56 vertices. It has 84 edges, and a Euler characteristic of -4. It is shown to the right.

Its Petrie polygons have 8 edges.

Its rotational symmetry group is PSL(2,7), and so it can be used as the basis of a Cayley diagram for PSL(2,7).

Antipodal Vertices

Each vertex is antipodal to one other vertex. Three examples of pairs of antipodal vertices are shown by pairs of coloured dots in the figure to the left. It can also be shown by comparison with the dual polyhedron S³:{3,7}, whose faces form antipodal pairs.

Antipodal Faces

If we make one face red, then each face sharing an edge with a red face yellow, then each face sharing an edge with a yellow face green, we find that two faces remain. These are shown blue in the diagram to the left. The two blue faces are also antipodal to each other. Thus the faces form mutually antipodal threesomes.

We realise the faces must form antipodal threesomes if we consider the Sylow-7-subgroups of its rotational symmetry group, which has 168 elements (in fact it is PSL(2,7)). This group must have eight conjugate C7s as its Sylow-7-subgroups. But the polyhedron has 24 heptagonal faces. So when we rotate one heptagonal face about its centre, we must also be rotating two other heptagonal faces about their centres.

This is discussed further in the page Rotating S³:{7,3}.

Antipodal Edges

Each edge is antipodal to three other edges. An examples of a foursome of antipodal edges is shown in green in the figure to the left.

You can click on any of these three images to see a larger version.

A similar but irregular map

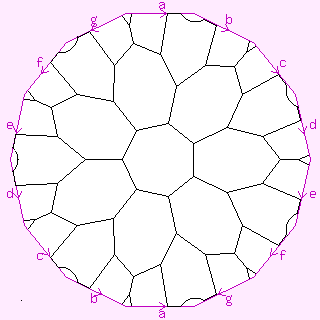
To the right is what appears to be another view of this map. But this is a different map, one which is not edge-transitive. It has the same numbers of vertices, faces and edges as the regular {7,3}, but its faces are not all equivalent, in particular it does not have threesomes of mutually antipodal faces.