Rotating S³:{7,3}

S³:{7,3} is a regular map with 24 heptagonal faces, three meeting at each of its 56 vertices, and 84 edges. Its rotational symmetry group is PSL(2,7).

This page considers what happens to it when we rotate it about the centre of one of its faces, fixing that face.

Comparison with a Dodecahedron

We start be describing what happens when we rotate a dodecahedron in a similar way.

The face whose centre we are rotating about remains in its plane, as does the opposite face. If we rotated our face clockwise through 2π/5, we find that the opposite face has rotated counterclockwise through 2π/5. The rotation is smooth and continuous, and acts on all parts of the dodecahedron: vertices, edges, and faces. After rotation through 2π/5, it looks as it did at the start. This is a symmetry operation of order 5. The dodecahedron's being embedded in Euclidean 3-space makes it clear that this must happen.

But S³:{7,3} does not embed nicely (retaining all its symmetry) in 3-space. A rotation acts continuously on its vertices, but not on its edges. If we rotate it through 2π, each vertex follows a continuous path, and there are eight of these paths, with seven vertices lying on each. The edges however cannot be followed as the structure rotates.

The lack of continuity is not peculiar to S³:{7,3}, it is a property of all regular maps except those in S⁰ and C¹. It is not what I want to discuss here.

What seems strange about S³:{7,3}

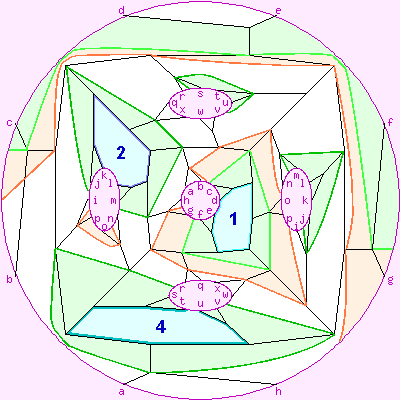
The diagram to the right is S³:{7,3}, coloured to show what happens as we rotate it about the centre of a face. When we rotate it clockwise about the face numbered 1:

• The vertices of that face obviously move clockwise one place, along the light blue line.
• The face numbered 1 is surrounded by a pastel green region, which is surrounded by a light green line. The seven vertices on that line each move one place clockwise along it.
• This pastel green is surrounded by a salmon region, which is surrounded by an orange line. The 14 vertices on the orange line each move two places along it. It is not appropriate to say thet the move "clockwise": each moves with the salmon region to its right hand.
• There are two other faces shown in pastel blue, numbered 2 and 4. The vertices of those faces move clockwise arond those faces, as shown by the blue lines, two and four places respectively.
• Those faces are surrounded by pastel green regions, which are surrounded by green lines. The vertices on those green lines move as shown by the green lines, two places clockwise and four places clockwise respectively.

If we trace a path along the edges of S³:{7,3}, turning left, left, left, right, left, left, left, right, etc., at successive vertices, we obtain a 28-sided polygon such as the one shown to the left. There are 24 such polygons in all. A set of antipodes comprises three faces and three of these polygons.

If we draw an antipodal set of three of these polygons, we find that any two of them have half of their edges in common, as shown to the right. Note that the orange polygon of this diagram runs close to the orange, and the orange and red, circuits of the two diagrams above it.

The diagram to the right has another interesting property. Suppose we consider only the polygons, and ignore the underlying S³:{7,3}, as shown to the left. Where all three polygons meet, place a vertex. If two of these vertices are directly connected by two coincident polygons, consider this as an edge. We now have the regular map S³:{14,3}