The Genus-3 Regular Map {14,3}

This genus-3 regular map has three 14-sided faces, all three meeting at each of its 14 vertices. It has 21 edges, and a Euler characteristic of -4. It is shown to the right.

Its Petrie polygons have six edges. Its Petrie dual is S¹{6,3}_(1,3).

Each 14-gon shares seven edges with each of the others, and all three faces meet at each vertex.

Regarded as a graph, it is the Heawood graph.

Its dual is S³{3,14}.

The diagram was constructed from that for S3:{7,3} by choosing three antipodal faces, and making them red, green, and blue;
making the face next to each red face light red, etc.;
merging all the light red faces with the red one, and removing internal lines; and the same for green and blue;
straightening and tidying the remaining edges. The resulting diagram shows no symmetry. There is probably a more symmetrical way to portray this map in two-space.

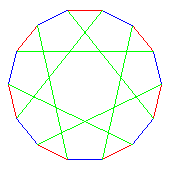
The edges of this map can be 3-coloured, as shown to the right.

This diagram can be regarded as a Cayley diagram of D14, with three generators of order 2 (of which any two would have been sufficient).

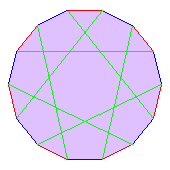
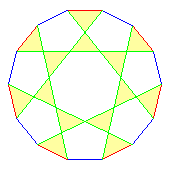
This coloured graph can be drawn on the plane, with its arcs crossing, as shown in the first diagram below. If we then colour in the three faces, we get the next three diagrams. Admittedly this is somewhat meaningless drawn like this on the wrong surface, but it is pretty.

   

The Symmetry Group of {14,3}

The rotational symmetry group is the Frobenius group of order 42, C7⋊C6, with elements of orders 1.2⁷.3¹⁴.6¹⁴.7⁶. Thus it has no symmetries of order 14.

This may seem surprising, as the faces have 14 sides. What happens when we rotate one of the 14-sided faces?

We find that this is not possible. We cannot rotate the polyhedron in such a way as to rotate one of its 14-sided faces by 1/14 of a turn (1/7 of a turn is no problem). Here is what happens if we try.

Start by labelling the vertices of the map from 0 to 13, in order as we follow the perimeter of a 14-sided face. Now recall that we have described the map as "regular", so by our definition it must be half-edge transitive, so it must be possible to rotate it so as to move the edge now labelled 0-1 to where the edge 1-2 was. We might expect that the edge 1-2 would in turn move to where 2-3 was, and so on. But see what does happen to the other edges as we do this. We find we have permuted the vertices: (0 1 2 7 6 5)(3 8 11 4 13 10)(9 12), and thus the edges: (0-1 1-2 2-7 7-6 6-5 5-0) (2-3 7-8 6-11 5-4 0-13 1-10) (3-4 8-13 11-10 4-3 13-8 10-11) (8-9 11-12 4-9 13-12 10-9 3-12). These permutations have order 6.

How is this impossibility of mapping a face to itself compatible with the claim that the symmetries of the polyhedron are face-transitive? Observe that the faces' 14 vertices are all 14 vertices of the whole polyhedron. This means that any permutation whatever of the vertices of the polyhedron must fix all the faces; so we do indeed have face-transitivity.

Relationship to {7,3}

{14,3} can be obtained from {7,3} as described at Rotating S3:{7,3}.