There is one regular map with four squares meeting at each vertex for each pair of non-negative integers a,b (except for 0,0). Each has a number of faces equal to a2+b2. Regular maps for integer pairs a,b with a<b exist, but are not shown here; they are the enantiomorphs of those for b,a.
All these regular maps are all self-dual.
The notation {4,4}(a,b) is consistent with that used in ARM, page 18.
ARM disallows (in our notation) {4,4}(1,0), in which the single square shares two edges with itself; and {4,4}(1,1), in which each of the two squares shares each of its vertices (but no edge) with itself.
Any {4,4} can be cantellated, yielding a {4,4} with twice as many vertices, faces and edges.
| designation | no. of squares | picture | V F E Eu | dual | rotational symmetry group | comments | |
|---|---|---|---|---|---|---|---|
| {4,4}(1,0) | 1 |  | 1 1 2 0 | self-dual | C4 |
 | |
| {4,4}(1,1) | 2 |  | 2 2 4 0 | self-dual | D8 |
| |
| {4,4}(2,0) | 4 |  | 4 4 8 0 | self-dual self-Petrie dual | C22⋊C4 | K4,4 |  |
| {4,4}(2,1) | 5 |  | 5 5 10 0 | self-dual | Frob20 ≅ C5⋊C4 | K5
| |
| {4,4}(2,2) | 8 |  | 8 8 16 0 | self-dual self-Petrie dual | ? | ||
| {4,4}(3,0) | 9 |  | 9 9 18 0 | self-dual | C32⋊C4 | ||
| {4,4}(3,1) | 10 |  | 10 10 20 0 | self-dual | (C5⋊C4)×C2 |  | |
| {4,4}(3,2) | 13 |  | 13 13 26 0 | self-dual | C13⋊C4 | | |
| {4,4}(4,0) | 16 |  | 16 16 32 0 | self-dual | C42⋊C4 | ||
| {4,4}(4,1) | 17 |  | 17 17 34 0 | self-dual | C17⋊C4 | | |
| {4,4}(3,3) | 18 |  | 18 18 36 0 | self-dual | ? | ||
| {4,4}(4,2) | 20 |  | 20 20 40 0 | self-dual | ? | | |
| {4,4}(4,3) | 25 |  | 25 25 50 0 | self-dual | ? | | |
| {4,4}(5,0) | 25 |  | 25 25 50 0 | self-dual | C52⋊C4 | ||
| {4,4}(5,1) | 26 |  | 26 26 52 0 | self-dual | ? | | |
| {4,4}(5,2) | 29 |  | 29 29 58 0 | self-dual | C29⋊C4 | | |
| {4,4}(4,4) | 32 | 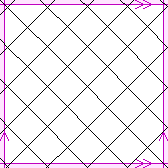 | 32 32 64 0 | self-dual | ? | ||
| {4,4}(5,3) | 34 |  | 34 34 68 0 | self-dual | ? | | |
| {4,4}(6,0) | 36 |  | 36 36 72 0 | self-dual | ? | ||
| {4,4}(6,1) | 37 |  | 37 37 74 0 | self-dual | C37⋊C4 | | |
| {4,4}(6,2) | 40 |  | 40 40 80 0 | self-dual | ? | | |
| {4,4}(5,4) | 41 |  | 41 41 82 0 | self-dual | ? | | |
| {4,4}(6,3) | 45 |  | 45 45 90 0 | self-dual | ? | | |
| {4,4}(7,0) | 49 |  | 49 49 98 0 | self-dual | C72⋊C4 | ||
| {4,4}(7,1) | 50 |  | 50 50 100 0 | self-dual | C50⋊C4 | | |
| {4,4}(5,5) | 50 |  | 50 50 100 0 | self-dual | ? |
The pink lines, arrows, and shading are explained by the page Representation of 2-manifolds.
Regular Maps in the Torus, with Hexagonal Faces
Regular Maps in the Torus, with Triangular Faces
Index to other pages on regular maps;
indexes to those on
S0
C1
S1
S2
S3
S4.
Some Cayley diagrams drawn on the torus.
Some pages on groups
Copyright N.S.Wedd 2009