Regular Maps in the Torus, with Hexagonal Faces
Schläfli symbol {6,3}(a,b)
The regular maps with three hexagons meeting at each vertex are more complicated than
those with four squares. They can all be generated from pairs of number of the form
a,b where a and b are either both odd or both even. The number
of faces of these regular maps is given by (a2+3*b2)/4.
More than one such pair can generate the same regular regular map, for example
{6,3}(2,4), {6,3}(5,3), and {6,3}(7,1) are all the
same regular map, with 13 faces. I have arbitrarily chosen to list them in ascending
order of the first parameter, which is necessarily also descending order of the second
parameter.
Most of these regular map are chiral, and so occur as enantiomorphic pairs. Only one
(arbitrarily chosen) member of each such pair is shown.
The notation {6,3}(a,b) used here is not
consistent with that used in ARM, page 19. Where ARM
writes {6,3}(s,0) we write {6,3}(s,s), and where ARM writes
{6,3}(s,s) we write {6,3}(0, 2s).
ARM disallows regular maps which (in our notation) are not of either of the forms
{6,3}(s,s) and {6,3}(0, 2s), because they lack "full
reflexional symmetry", i.e. they are chiral. It also disallows (in our
notation) {6,3}(1,1), in which the single hexagon
shares three edges with itself.
| designation | no. of
hexagons | picture | V
F
E
Eu | dual
Petrie dual | rotational
symmetry
group | comments |
|---|
| {6,3}(1,1) {6,3}(2,0) | 1 |  | 2
1
3
0 | {3,6}(1,1)
3-hosohedron | D6 |

 |
|---|
| {6,3}(0,2) {6,3}(3,1) | 3 |  | 6
3
9
0 | {3,6}(0,2)
self-Petrie dual | D6×C3 | K3,3 Water, gas, and electricity
The three-rung Möbius ladder S86. |
|---|
| {6,3}(2,2) {6,3}(4,0) | 4 |  | 8
4
12
0 | {3,6}(2,2)
cube | S4 | |  |
|---|
| {6,3}(1,3) {6,3}(4,2) {6,3}(5,1) | 7 |  | 14
7
21
0 | {3,6}(1,3)
S3{14,3} | Frob42
≅
C7⋊C6 |  |
|---|
| {6,3}(3,3) {6,3}(6,0) | 9 |  | 18
9
27
0 | {3,6}(3,3)
self-Petrie dual | ? | the Pappus graph |
|---|
| {6,3}(0,4) {6,3}(6,2) | 12 | 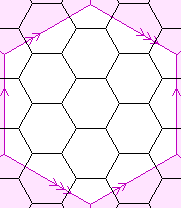 | 24
12
36
0 | {3,6}(0,4)
S4{12,3} | ? | the Nauru graph |
|---|
| {6,3}(2,4) {6,3}(5,3) {6,3}(7,1) | 13 |  | 26
13
39
0 | {3,6}(2,4)
| ? | the F26A graph 
|
|---|
| {6,3}(4,4) {6,3}(8,0) | 16 |  | 32
16
48
0 | {3,6}(4,4)
S3{8,3} | ? | The Dyck graph |
|---|
| {6,3}(1,5) {6,3}(7,3) {6,3}(8,2) | 19 |  | 38
19
57
0 | {3,6)(1,5)
| C19⋊C3 |  |
|---|
| {6,3}(3,5) {6,3}(6,4) {6,3}(9,1) | 21 |  | 42
21
63
0 | {3,6)
(3,5} | ? |  |
|---|
| {6,3}(5,5) {6,3}(10,0) | 25 |  | 50
25
75
0 | {3,6}(5,5)
| ? | |
|---|
| {6,3}(0,6) {6,3}(9,3) | 27 | 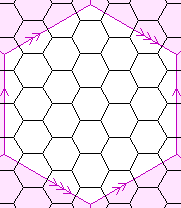 | 54
27
81
0 | {3,6}(0,6)
| ? | |
|---|
| {6,3}(2,6) {6,3}(8,4) {6,3}(10,2) | 28 |  | 56
28
84
0 | {3,6}(2,6)
| ? |  |
|---|
| {6,3}(4,6) {6,3}(7,5) {6,3}(11,1) | 31 |  | 62
31
93
0 | {3,6}(4,6)
| ? |  |
|---|
| {6,3}(6,6) {6,3}(12,0) | 36 |  | 72
36
108
0 | {3,6}(6,6)
| ? | |
|---|
| {6,3}(1,7) {6,3}(10,4) {6,3}(11,3) | 37 |  | 74
37
111
0 | {3,6}(1,7)
| ? |  |
|---|
| {6,3}(3,7) {6,3}(8,6) {6,3}(9,5) {6,3}(12,2) | 39 |  | 78
39
117
0 | {3,6}(3,7)
| ? | 
|
|---|
| {6,3}(5,7) {6,3}(13,1) | 43 |  | 86
43
126
0 | {3,6}(5,7)
| ? |  |
|---|
| {6,3}(0,8) {6,3}(12,4) | 48 | 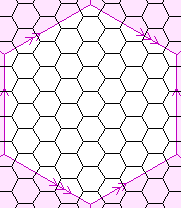 | 96
48
144
0 | {3,6}(0,8)
| ? | |
|---|
| {6,3}(7,7) {6,3}(14,0) | 49 |  | 98
49
147
0 | {3,6}(7,7)
| ? | |
|---|
| {6,3}(2,8) {6,3}(11,5) {6,3}(13,3) | 49 | 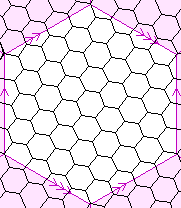 | 98
49
147
0 | {3,6}(2,8)
| ? |  |
|---|
The pink lines, arrows, and shading are explained by the page
Representation of 2-manifolds.
Regular Maps in the Torus, with Square Faces
Regular Maps in the Torus, with Triangular Faces































