Regular Maps in the Torus, with Triangular Faces
Schläfli symbol {3,6}(a,b)
The regular maps with six triangles meeting at each
vertex are the duals of those with three hexagons.
As for {6,3}(a,b), a and b
must be either both odd or both even. The number of
faces of these polyhedra is given by
(a2+3*b2)/2.
The notation used here {3,6}(a,b) is not
consistent with that used in ARM,
and is as described above for {6,3}(a,b). Thus our
{6,3}(a,b) is the dual of our {3,6}(a,b).
ARM also disallows (in our notation)
{3,6}(1,1), in which each of the
two triangles shares each of its vertices (but no edge) with itself.
| designation | no. of
triangles | picture | V
F
E
Eu | dual
Petrie dual | rotational
symmetry
group | comments |
|---|
| {3,6}(1,1} {3,6}(2,0) | 2 |  | 1
2
3
0 | {6,3}(1,1)
hemi-3-hosohedron | D6 |
 |
|---|
| {3,6}(0,2) {3,6}(3,1) | 6 |  | 3
6
9
0 | {6,3}(0,2)
C5{6,6} | D6×C3 | |
|---|
| {3,6}(2,2) {3,6}(4,0) | 8 |  | 4
8
12
0 | {6,3}(2,2)
C4{4,6} | S4 | |
|---|
| {3,6}(1,3) {3,6}(4,2) {3,6}(5,1) | 14 |  | 7
14
21
0 | {6,3}(1,3}
| Frob42
≅
C7⋊C6 | K7 
|
|---|
| {3,6}(3,3) {3,6}(6,0) | 18 |  | 9
18
27
0 | {6,3}(3,3)
| ? | K3,3,3 |
|---|
| {3,6}(0,4) {3,6}(6,2) | 24 |  | 12
24
36
0 | {6,3}(0,4)
| ? | |
|---|
| {3,6}(2,4) {3,6}(5,3) {3,6}(7,1) | 26 |  | 13
26
39
0 | {6,3}(2,4)
| ? | the Paley order-13 graph 
|
|---|
| {3,6}(4,4) {3,6}(8,0) | 32 |  | 16
32
48
0 | {6,3}(4,4)
| ? | the Shrikhande graph |
|---|
| {3,6}(1,5) {3,6}(7,3) {3,6}(8,2) | 38 |  | 19
38
57
0 | {6,3}(1,5)
| C19⋊C3 |  |
|---|
| {3,6}(3,5) {3,6}(6,4) {3,6}(9,1) | 42 |  | 21
42
63
0 | {6,3}(3,5)
| ? |  |
|---|
| {3,6}(5,5) {3,6}(10,0) | 50 |  | 25
50
75
0 | {6,3}(5,5)
| ? | |
|---|
The following figures have more than 50 faces; they are included because their duals are above. |
| {3,6}(0,6) {3,6}(9,3) | 54 |  | 27
54
81
0 | {6,3}(0,6)
| ? | |
|---|
| {3,6}(2,6) {3,6}(8,4) {3,6}(10,2) | 56 |  | 28
56
84
0 | {6,3}(2,6)
| ? |  |
|---|
| {3,6}(4,6) {3,6}(7,5) {3,6}(11,1) | 62 |  | 31
62
93
0 | {6,3}(4,6)
| ? |  |
|---|
| {3,6}(6,6) {3,6}(12,0) | 72 |  | 36
72
108
0 | {6,3}(6,6)
| ? | |
|---|
| {3,6}(1,7) {3,6}(10,4) {3,6}(11,3) | 74 |  | 37
74
111
0 | {6,3}(1,7)
| ? |  |
|---|
| {3,6}(3,7) {3,6}(8,6) {3,6}(9,5) {3,6}(12,2) | 78 |  | 39
78
117
0 | {6,3}(3,7)
| ? |  |
|---|
| {3,6}(5,7) {3,6}(13,1) | 86 |  | 43
86
126
0 | {6,3}(5,7)
| ? |  |
|---|
| {3,6}(0,8) {3,6}(12,4) | 96 |  | 48
96
144
0 | {6,3}(0,8)
| ? | |
|---|
| {3,6}(7,7) {3,6}(14,0) | 98 | 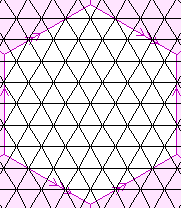 | 49
98
147
0 | {6,3}(7,7)
| ? | |
|---|
| {3,6}(2,8) {3,6}(11,5) {3,6}(13,3) | 98 |  | 49
98
147
0 | {6,3}(2,8)
| ? |  |
|---|
The pink lines, arrows, and shading are explained by the page
Representation of 2-manifolds.
Regular Maps in the Torus, with Square Faces
Regular Maps in the Torus, with Hexagonal Faces





























