Holes and Petrie Polygons

A Petrie polygon is a polygon found in a regular map by travelling along its edges, turning sharp left and sharp right at alternate vertices.

A hole has a general definition, which applies to polytopes in any number of dimensions. But for our 2-dimensional purposes, we consider it as a polygon found in a regular map by travelling along its edges, taking the second-sharpest left at each vertex.

These concepts are related, and can be generalised as follows.
A 1st-order hole is just a face.
A 1st-order Petrie polygon is an ordinary Petrie polygon.
A 2nd-order hole is an ordinary hole.
A 2nd-order Petrie polygon is found by travelling along the edges of a regular map taking alternately the second-sharpest left and the second-sharpest right.
A 3rd-order hole is found by travelling along the edges of a regular map always taking the third-sharpest left.
A 3nd-order Petrie polygon is found by travelling along the edges of a regular map taking alternately the third-sharpest left and the third-sharpest right.
A 4th-order hole is found by travelling along the edges of a regular map always taking the fourth-sharpest left.
Etc.

This can be summarised:

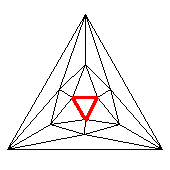
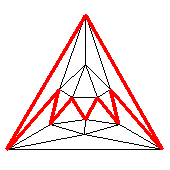
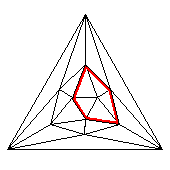
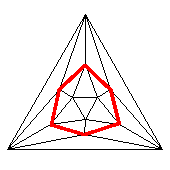
polygon summary
of route		 minimum
edges/vertex
for this to be
meaningful		 symbol
used in
these
pages
VertexV
EdgeE
FaceL,F
Petrie polygonL,R,3P
HoleL2,4H
2nd-order Petrie polygonL2,R2,5P2
3rd-order holeL3,6H3
3rd-order Petrie polygonL3,R3,7P3
4th order HoleL4,8H4
4th-order Petrie polygonL4,R4,9P4
etc.
Icosahedron with one face shown in red. Icosahedron with one Petrie polygon shown in red.
Icosahedron with one hole shown in red. Icosahedron with one 2nd-order Petrie polygon shown in red.

We will use the abbeviations in the final column of the table when specifying the sets of antipodes of a polyhedron. Thus we would list the antipodal sets of the icosahedron as

(2V, 2H, P)two vertices, two holes, one Petrie polygon
(2E)two edges
(2F, P2)two faces, one 2nd-order Petrie polygon

Index to Regular Maps
Glossary for Regular Maps