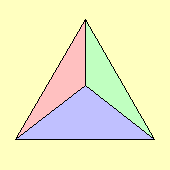See also Graphs and Regular Maps
identified with regular maps | not identified with regular maps | known not to be regular
When I first became interested in regular maps, I did not know what they were called. But as each one involves a symmetric graph, I realised that I could try to find them by choosing some symmetric graph, maybe from Wikipedia's "gallery of named graphs", and trying to find a way to embed it regularly in a compact 2-manifold.
The page lists some symmetric graphs, and for each which I know how to embed regularly in some manifold, gives a link to a page where I show it as a regular map.
Some named graphs can be embedded nicely in a manifold, but not in a fully regular way. For example, the Franklin graph can be embedded in the projective plane, where it is seen to be a truncated hemi-octahedron, which is not face-transitive. A few of these are listed in the main table of this page, but I have not tried to list irregular named graphs systematically.
| Name of graph (link to wikipedia) |
Picture of graph | Valency | Vertices | Edges | Full symmetry group of graph |
Rotational symmetry group of regular map |
Schläfli symbol (link to polyhedron) |
Picture of regular map | Faces of regular map |
|---|---|---|---|---|---|---|---|---|---|
| Cube |  |
3 | 8 | 12 | 48 S4×C2 |
24 S4 |
{4,3} |  |
6 squares |
| Cycle graph |  |
2 | n | n | 2n D2n |
n Cn |
{5,2} |  |
2 pentagons |
| Desargues graph |  |
3 | 20 | 30 | 240 S5×C2 |
60 A5 |
C6:{10,3}10 |  |
6 decagons |
| Dodecahedron |  |
3 | 12 | 30 | 120 S5 |
60 A5 |
{3,5} |  |
12 pentagons |
| Dyck graph |  |
3 | 32 | 48 | 192 | 96 | {6,3}(4,4) |  |
16 hexagons |
| 96 | S3{8,3} |  |
12 octagons | ||||||
| F26A graph |  |
3 | 26 | 39 | 78 | 78 | {6,3}(2,4) |  |
13 hexagons |
| Franklin graph |  |
3 | 12 | 18 | 48 S4×C2 |
26 S4 |
Not regular. Can be embedded in the projective plane, as a truncated hemi-octahedron, having .. | .. 3 squares and 4 hexagons | |
| Heawood graph |  |
3 | 14 | 21 | 336 PGL(2,7) |
21 C7⋊C3 |
S3:{14,3} |  |
Not quite regular. 3 14-gons |
| Icosahedron |  |
3 | 20 | 30 | 120 A5×C2 |
60 A5 |
{3,5} |  |
20 triangles |
| K1 |  |
0 | 0 | 0 | 1 S1 |
1 S1 |
{0,0} |  |
1 point-bounded face |
| K2 |  |
1 | 2 | 1 | 2 S2 |
2 S2 |
{2,1} |  |
1 digon |
| K3 |  |
2 | 3 | 3 | 6 S3 |
6 S3 |
{3,2} |  |
2 triangles |
| K4 |  |
3 | 4 | 6 | 24 S4 |
12 A4 |
{3,3} |  |
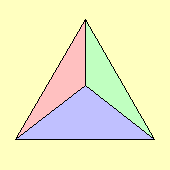4 triangles |
| K5 |  |
4 | 5 | 10 | 120 S5 |
20 C5⋊C4 |
{4,4}(2,1) |  |
5 squares |
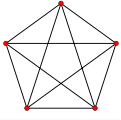
| K6 |  |
5 | 6 | 15 | 720 S6 |
60 A5 |
C1:{3,5}, the hemi-icosahedron |  |
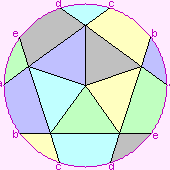10 triangles |
| K7 |  |
6 | 7 | 21 | 5,040 S7 |
42 C7⋊C6 |
{3,6}(1,3) |  |
14 triangles |
| K8 |  |
7 | 8 | 28 | 40,320 S8 |
56 (C2×C2×C2)⋊C7 |
S7:{7,7} and its dual S7:{7,7} |  |
8 heptagons |
| Kn | See a list of complete graphs embedded as regular maps. | ||||||||
| K3,3 Utility |
 |
3 | 6 | 9 | 72 (S3×S3)⋊C2 |
18 D6×C3 |
{6,3}(0,2) |  |
3 hexagons |
| K4,4 |  |
4 | 4 | 8 | 1,152 (S4×S4)⋊C2 |
16 C22⋊C4 |
{4,4}(2,2) |  |
8 squares |
| 16 | S3{8,4|4} |  |
4 octagons | ||||||
| K5,5 | 4 | 10 | 25 | 28,800 | 50 | S6:{10,5} | 5 hexagons | ||
| K6,6 | 5 | 12 | 36 | 1,036,000 | 72 | S4:{4,6} |  |
18 squares | |
| K7,7 | 6 | 14 | 49 | 50,803,200 | 98 | S15:{14,7} | 7 14-gons | ||
| K2,2,2 |  |
4 | 6 | 12 | 96 (S2×S2×S2)⋊S3 |
12 A4 |
{3,4} |  |
8 triangles |
| K3,3,3 |  |
6 | 9 | 27 | 1,296 (S3×S3×S3)⋊S3 |
54 | {3,6}(3,3) |  |
18 triangles |
| K4,4,4 |  |
8 | 12 | 48 | 82,944 (S4×S4×S4)⋊S3 |
96 | S3:{3,8}, the dual of the Dyck map |  |
12 octagons |
| K5,5,5 | 10 | 15 | 75 | 10,368,000 | 96 | S6:{3,10} | 50 triangles | ||
| Klein graph |  |
3 | 56 | 84 | 336 PGL(2,7) |
168 PSL(2,7) |
S3:{7,3}, the Klein map |  |
24 heptagons |
| Möbius-Kantor graph |  |
3 | 16 | 24 | 96 | 48 | S2:{8,3} |  |
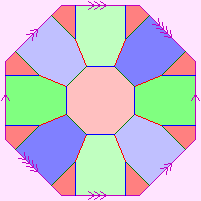6 octagons |
| Nauru graph |  |
3 | 24 | 36 | 144 S4×D6 |
72 | {6,3}(0,4) |  |
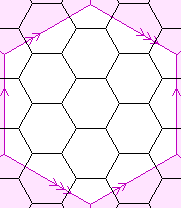12 hexagons |
| Octahedron | See K2,2,2 above | ||||||||
| Paley order-13 graph |  |
6 | 13 | 39 | 78 | 78 | {3,6}(2,4) |  |
26 triangles |
| Pappus graph |  |
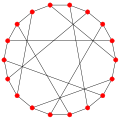3 | 18 | 27 | 216 | 54 | {6,3}(3,3) |  |
9 hexagons |
| Petersen graph |  |
3 | 10 | 15 | 120 S5 |
60 A5 |
C1:{5,3}, the hemidodecahedron |  |
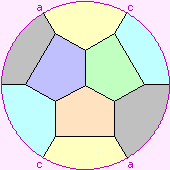6 pentagons |
| Shrikhande graph |  |
6 | 16 | 48 | 192 | 96 | {3,6}(4,4) |  |
32 triangles |
| Tetrahedron | See K4 above | ||||||||
These either don't exist as regular maps, or do but I don't know how.
| Biggs-Smith graph |  |
3 | 102 | 153 | 2448 PSL(2,17) |
? | |
| Clebsch graph also called the Greenwood-Gleason graph |
 |
5 | 16 | 40 | 1920 | (20 squares) | |
| Coxeter graph |  |
3 | 28 | 42 | 336 PGL(2,7) |
(12 heptagons) | |
| 10-crown |  |
4 | 10 | 20 | 80 | (8 pentagons, but this graph is bipartite) | |
| Double-star snark |  |
3 | 30 | 45 | ? | 3 30-gons | |
| Foster graph |  |
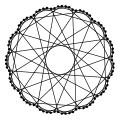3 | 90 | 135 | 4320 | ? | |
| Hall-Janko graph |  |
? | 100 | ? | ? | ? | |
| Higman-Sims graph |  |
22 | 100 | 1100 | 88,704,000 HS⋊C2) |
? | |
| Hoffman-Singleton graph |  |
7 | 50 | 175 | 252,000 PSU(3,52)⋊C2 |
? | |
| Horton graph |  |
3 | 96 | 144 | 96 S4×C2×C2 |
Not the same as {6,3}(0,8) | |
| Tutte-Coxeter graph |  |
3 | 30 | 45 | 1,440 Aut(S6) |
? |
More on Regular Maps
.Copyright N.S.Wedd 2009
All the images on this page were taken from Wikipedia.