This page discusses what we mean by "regular", when applied to a polyhedron or regular map. It starts with some simple examples, of polyhedra and of tilings of the torus with squares.

The cube is regular by all standards. All its faces are regular and interchangeable, and all its vertices are regular and interchangeable.
Its Petrie polygons all have six edges.
It has mirror symmetry. Its rotational symmetry group is S4, with 24 elements (twice its number of edges), and its full symmetry group (including reflections) is S4×C2, with 48 elements.
This image, and the next two, are copied from Wikipedia.

The cuboctahedron is not regular (it is "quasiregular"). Its faces are all regular, but it has two different kinds of face. Its vertices are all interchangeable, but are not regular.
Its Petrie polygons all have eight edges. Its holes all have six edges.
It has mirror symmetry. Its rotational symmetry group is S4, with 24 elements (equal to its number of edges), and its full symmetry group (including reflections) is S4×C2, with 48 elements.

The rhombic dodecahedron is the dual of the cuboctahedron. It is not regular. Its faces are interchangeable, but are not regular, they are rhombi rather than squares. Its vertices are regular, but are not interchangeable: some have three edges, some have four.
Its Petrie polygons all have eight edges.
Like its dual, it has mirror symmetry. Its rotational symmetry group is S4, with 24 elements (equal to its number of edges), and its full symmetry group (including reflections) is S$×C2, with 48 elements.
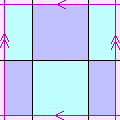
This regular map may or may not be regarded as regular. Its faces are interchangeable, and are regular in shape. Its vertices are interchangeable, and are regular in shape. However, if we walk "east" along an edge until we return to where we have started we traverse two edges, whereas if we walk north we traverse one. So the north-south edges are not interchangeable with the east-west edges, and so rotating it through a right angle about the centre of a face is not a symmetry operation.
Its Petrie polygons all have four edges. One of its holes has two edges, two others have one edge each.
It has mirror symmetry. Its rotational symmetry group is C2×C2, with 4 elements (equal to its number of edges), and its full symmetry group is C2×C2×C2, with 8 elements.
(This is not the only wat to tile a torus with two squares. {4,4}(1,1) is fully regular.)

This regular map may or may not be regarded as regular. Its faces are interchangeable, and are regular in shape. Its vertices are interchangeable, and are regular in shape. However, each face has two vertices where it has corner-wise contact with itself, and two where it does not; so rotating it through a right angle about the centre of a face is not a symmetry operation.
One of its Petrie polygons has six edges, three others each have two edges. Its holes all have three edges.
It has mirror symmetry. Its rotational symmetry group is D6, with 6 elements (equal to its number of edges), and its full symmetry group is D12, with twelve elements.

This regular map may or may not be regarded as regular. Its faces are interchangeable, and are regular. Its vertices are interchangeable, and are regular.
Its Petrie polygons all have ten edges. Its holes all have five edges.
It does not have mirror symmetry. Its rotational symmetry group is C5⋊C4, with 20 elements (twice its number of edges), and its full symmetry group is the same, as it has no reflections.
My personal view is that, of the things listed above, the cube and the "fives squares" are regular, the other four are not.
The cuboctahedron's faces are not all the same; the rhombic dodecahedron's vertices are not all the same; the two-square figure has faces which are, in a sense, rectangular rather than square; similarly the three-square figure's faces are rhombic. However the cube and the five-square figure appear to me to be what I mean by "regular". The latter is chiral, but I don't regard that as making it irregular.
I observe that these two have rotational symmetry groups with twice as many elements as they have edges, and the other things do not. But let's consider things in more detail.
In the study of polytopes, a "flag" consists of a vertex, and an edge incident to that vertex, and a face incident to that edge, and a polyhedron incident to that edge, and a polytope incident to that polyhedron, and so on until we have reached the entire polytope. But here, we are only concerned with things that are embedded in a 2-space; so a flag is merely a vertex and an incident edge and an incident face. This there are four flags for each edge.
Those polyhedra, and regular maps, which are regarded by everyong as regular are all "flag-transitive". That means that, for any pair of flags, there is some symmetry operation which maps onne to the other.
The diagrams below each show an edge, with all four of its flags, and some flags of adjacent edges. In each diagram, two flags are shown in the same colour if there is a symmetry operation (of the whole polyhedron or map) which maps one to the other.
 Type 0.
Type 0.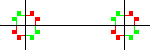 Type 1a.
Type 1a. Type 1b.
Type 1b. Type 2.
Type 2. Type 3.
Type 3.Note that if we consider only the edge itself with its own four flags, types 1a and 1b are the same.
The phrase "half-edge transitive" is ambiguous. Edges of types 0, 1a, and 1b are definitely half-edge transitive. It is not clear users of whether users of this phrase intend to cover edges of types 2 and 3.
In this section we list the six polyhedra and regular maps shown above, and clasify them by the following criteria.
| Regular Map | Face | Vertex | Edge | Mirror | RSG | FSG | PPs | holes | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| tr. | rot. | tr. | rot. | tr. | type | /edge ratio | all =? | |||||
| Cube | Y | Y | Y | Y | Y | 0 | Y | 2 | 4 | Y | ||
| Cuboctahedron | N | Y | Y | N | Y | 2 | Y | 1 | 2 | Y | Y | |
| Rhombic dodecahedron | Y | N | N | Y | Y | 3 | Y | 1 | 2 | Y | ||
| Two squares | Y | N | Y | N | N | 1a | Y | 1 | 2 | Y | N | |
| Three squares | Y | N | Y | N | Y | 1a | Y | 1 | 2 | N | Y | |
| Five squares | Y | Y | Y | Y | Y | 1b | N | 2 | 2 | Y | Y | |
We see that the "five squares" map scores as high as the cube, except that
My definition of "regular map" is written to include the cube and the "five squares", but not the four other examples of maps given on this page.
Index to other pages on regular maps.
Copyright N.S.Wedd 2010