This page is obsolete. See the current version of Regular Maps in the orientable surface of genus 2

Regular Maps on the Genus-2 Orientable Manifold

This page shows some of the regular maps that can be drawn on the genus-2 orientable manifold. For the purpose of these pages, a "regular map" is defined here.

To draw these maps, we need a way of portraying the oriented genus-2 surface in flat 2-space. We may use any of the diagrams shown to the right (they are equivalent). The surface itself is shown in white, the pink letters show how the "cut edges" are to be joined up, and the light pink regions are not part of the surface. This is further explained by the page Representation of 2-manifolds.

The first two columns in the two tables below were created by listing every conceivable regular map {G,H} with V vertices F faces and E edges which would have Euler number -2. These are all listed below. The first table is for regular maps that exist, with links to pages about them; the second table is for combinations of G, H, V, F and E for which no regular map exists.

An image in the "thumbnail" column of the main table is a link to a page with more information about the regular map.

Regular Maps

Schläfli symbol C&D no.	V+F-E=Eu	thumbnail	dual Petrie dual	Rotational Symmetry Group	comments	qy
{8,3} R2.1′	16+6-24=-2		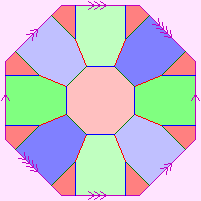{3,8} S3{12,3}	GL(2,3)		3
{3,8} R2.1	6+16-24=-2		{8,3} S8? :{12,8}
{6,4} R2.2′	6+4-12=-2		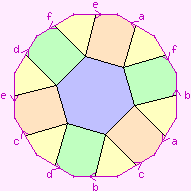{4,6} S3{12,4}	C3⋊D8		2
{4,6} R2.2	4+6-12=-2		{6,4} S4:{12,6}
{8,4} R2.3′	4+2-8=-2		{4,8} self-Petrie dual	Quasidihedral of order 16		1
{4,8} R2.3	2+4-8=-2		{8,4} S3:{8,8}4
{6,6} R2.5	2+2-6=-2		self-dual 6-hosohedron	D12		1
{8,8} R2.6	1+1-4=-2		self-dual 4-hemihosohedron	D8		½
{10,5} R2.4′	2+1-5=-2		{5,10} 5-hosohedron	D10		½
{5,10} R2.4	1+2-5=-2		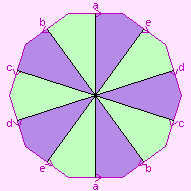{10,5} 5-hemihosohedron

Maps that do not have a regular form

Where the table below has a thumbnail image linking to a page, it is about an irregular map. Its faces all have the same number of edges, as do its vertices, but it is not half-edge transitive.

Schläfli symbol	V+F-E=Eu	thumbnail	dual	Evidence for non-existence, other comments
{7,3}	28+12-42=-2		{3,7}	S7
{3,7}	12+28-42=-2		{7,3}
{5,4}	10+8-20=-2		{4,5}	S5
{4,5}	8+10-20=-2		{5,4}
{9,3}	12+4-18=-2		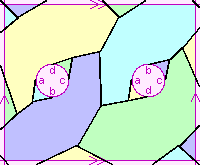{3,9}	The group would have to be C22⋊C9
{3,9}	4+12-18=-2		{9,3}
{5,5}	4+4-10=-2		self-dual	S5, E
{10,3}	10+3-15=-2		{3,10}	I have no proof
{3,10}	3+10-15=-2		{10,3}
{12,3}	8+2-12=-2		{3,12}	, D
{3,12}	2+8-12=-2		{12,3}
{18,3}	6+1-9=-2		{3,18}	proof
{3,18}	1+6-9=-2		{18,3}
{12,4}	3+1-6=-2		{4,12}	I have no proof
{4,12}	1+3-6=-2		{12,4}