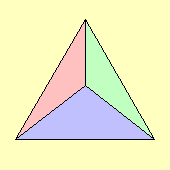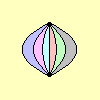This page shows all the regular polyhedra that can be drawn
on the genus-0 orientable manifold, the sphere. For the purpose
of these pages, a "regular polyhedron" is regarded as a
regular map on the sphere.
This definition gives five regular polyhedra, also known as
the five platonic solids; and some other less interesting things.
There are many better web pages about the five platonic solids,
for instance on Wikipedia, on
Wolfram, and
a page which lets you rotate them.
| name | Schläfli
symbol | picture | V
F
E
Eu | dual
Petrie dual | rotational
symmetry
group | Antipodes, etc. | Comments | qy |
|---|
| tetrahedron | {3,3} | 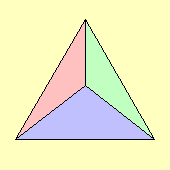 | 4
4
6
2 | self-dual
hemicube | A4 | Each face is antipodal to a vertex and vice versa; and each edge to an edge. Cantellation of the tetrahedron yields the octahedron. | These are the five "Platonic solids". 
| 2 |
|---|
| cube | {4,3} |  | 8
6
12
2 | octahedron
{6,3}(2,2} | S4 | Each face is antipodal to one face, each vertex to one vertex, and each edge to one edge. | 3 |
|---|
| octahedron | {3,4} |  | 6
8
12
2 | cube
C4{6,4} | S4 | Each face is antipodal to one face, each vertex to one vertex, and each edge to one edge. | 3 |
|---|
| dodecahedron | {5,3} |  | 20
12
30
2 | icosahedron
C6{10,3}5 | A5 | Each face is antipodal to one face, each vertex to one vertex, and each edge to one edge. | 6 |
|---|
| icosahedron | {3,5} |  | 12
20
30
2 | dodecahedron
C14{10,5} | A5 | Each face is antipodal to one face, each vertex to one vertex, and each edge to one edge. | 6 |
|---|
| The things below are not normally considered to be polyhedra.
However they fit my definition. |
n-hosohedron
(heptahosohedron, etc.) | {2,n} | 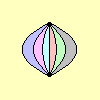 | 2
n
n
2 |
di-n-hedron
n=3: S1:{6,3}(1,1)
n=4: S1:{4,4}(1,1)
n=5: S2:{10,5}
n=6: S2:{6,6}
n=7: S3:{14,7}
n=8: S3:{8,8}2
| D2n |
n odd: Each face is antipodal to one edge and vice versa; each vertex is antipodal to the other vertex.
n even: Each face is antipodal to one face, each edge to one edge, and each vertex to the other vertex. |

The image uses 7 as an example value for n. | 1 |
|---|
di-n-hedron
(diheptagon, etc.) | {n,2} | 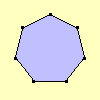 | n
2
n
2 | n-hosohedron
n odd: C1:{2n,2}
n even: self-Petrie dual
| D2n |
n odd: Each vertex is antipodal to one edge and vice versa; each face is antipodal to the other face.
n even: Each vertex is antipodal to one vertex, each edge to one edge, and each face to the other face. |

The image uses 7 as an example value for n. | 1 |
|---|
2-hosohedron,
digonal dihedron
| {2,2} |  | 2
2
2
2 | self-dual
self-Petrie dual | C2×C2 |
Each face is antipodal to the other face, each vertex to the other vertex, and each edge to the other edge. Cantellation of the 2-hosohedron yields the 4-hosohedron.
|
  | 1 |
|---|
monodigon
| {2,1} |  | 2
1
1
2 | dimonogon
self-Petrie dual | C2 |
Each vertex is antipodal to the other vertex; the face is antipodal to the edge and vice versa. |
   | ½ |
|---|
dimonogon
| {1,2} |  | 1
2
1
2 | monodigon
hemi-digonal hosohedron | C2 |
Each face is antipodal to the other face; the vertex is antipodal to the edge and vice versa. |
   | ½ |
|---|
edgeless map
| {0,0} |  | 1
1
0
2 | self-dual
self-Petrie dual | C1 |
The face is antipodal to the vertex and vice versa. There is no edge. Our definition of a regular map requires that each face must have the topology of a disk. So this is a valid regular map; but in all other manifolds there must be at least one edge. |
  | 0 |
|---|