This page shows all the regular maps that can be drawn in
the projective plane. For the purpose of these pages, a "regular
map" is defined here.
These include analogues of four of the five platonic solids,
each with half as many vertices, faces and edges. The
tetrahedron has no analogue in the projective plane.
| name | Schläfli
symbol | picture | V
F
E
Eu | dual
Petrie dual | symmetry
group | Comments | qy |
|---|
| hemi-cube | {4,3} |  | 4
3
6
1 | hemi-octahedron
tetrahedron | S4 |  | 1½ |
|---|
| hemi-octahedron | {3,4} |  | 3
4
6
1 | hemi-cube
self-Petrie dual | S4 |  | 1½ |
|---|
| hemi-dodecahedron | {5,3} | 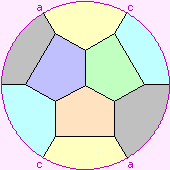
 | 10
6
15
1 | hemi-icosahedron
self-Petrie dual | S5 |
The Petersen graph.
If you take hemi-dodecahedra and glue them together five to an
edge, you will find that 57 of them form a regular polytope, the
57-cell,
Schläfli symbol {5,3,5}. Its symmetry group is PSL(2,19). 
| 3 |
|---|
| hemi-icosahedron | {3,5} | 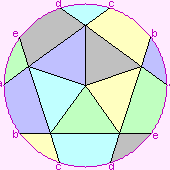 | 6
10
15
1 | hemi-dodecahedron
C5{5,5} | S5 |
If you take a hemi-icosahedron and glue another one to each face, and bend them
round so that three meet at each edge, you will find that the 11 of them form a
regular polytope, the 11-cell,
Schläfli symbol {3,5,3}. Its symmetry group is PSL(2,11). 
| 3 |
|---|
| hemi-hosohedron | {2,2n} |  | 1
n
n
1 | hemi-dihedron
n=2: S1:{4,4}(1,0)
n=3: S1:{3,6}(1,1)
n=4: S2:{8,8}
n=5: S2:{5,10}
n=6: S3:{12,12}
n=7: S3:{7,14}
| D4n |

 
The image uses 7 as an example value for n. | ½ |
|---|
| hemi-dihedron | {2n,2} |  
| n
1
n
1 | hemi-hosohedron
n odd: S0:{n,2}
n even: self-Petrie dual
| D4n |
  
The images use 7 as an example value for n. The second image only works for odd n. | ½ |
|---|
| hemi-digonal hosohedron | {2,2} |  | 1
1
1
1 | self-dual
dimonogon | C2×C2 |
   
 Cantellation of the hemi-digonal hosohedron yields the hemi-4-hosohedron.
| ½ |
|---|





















