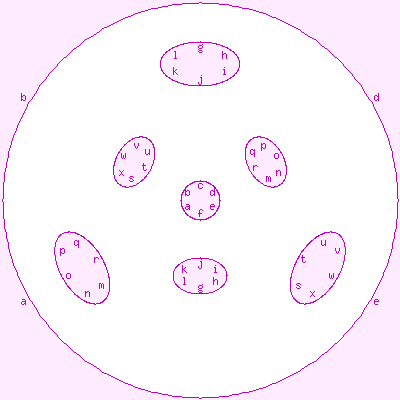
 To draw these maps, we need a way of portraying the oriented genus-4 surface
in flat 2-space. We use the diagram shown to the right, which can be regarded
as an octahedron with a tunnel connected each pair of opposite faces.
To draw these maps, we need a way of portraying the oriented genus-4 surface
in flat 2-space. We use the diagram shown to the right, which can be regarded
as an octahedron with a tunnel connected each pair of opposite faces.
This page shows just one (so far) of the regular maps that can be drawn on the genus-4 orientable manifold. For the purpose of these pages, a "regular map" is defined here.
 To draw these maps, we need a way of portraying the oriented genus-4 surface
in flat 2-space. We use the diagram shown to the right, which can be regarded
as an octahedron with a tunnel connected each pair of opposite faces.
To draw these maps, we need a way of portraying the oriented genus-4 surface
in flat 2-space. We use the diagram shown to the right, which can be regarded
as an octahedron with a tunnel connected each pair of opposite faces.
An image in the "thumbnail" column of the main table is a link to a page with more information about the regular map. Where the thumbnail image is shown on a grey background, the link is to a map that is not regular.
| Schläfli symbol C&D no. | V+F-E=Eu | thumbnail (link) | dual | Rotational Symmetry Group | comments | qy |
|---|---|---|---|---|---|---|
| {5,4} R4.2′ |
30+24-60=-4 | {4,5} ? |
A group of order 120 | ? | 12 | |
| {4,5} R4.2 |
24+30-60=-4 | {5,4} ? |
||||
| {6,4} R4.3′ |
18+12-36=-4 | {4,6} ? |
A group of order 72 | ? | 6 | |
| {4,6} R4.3 |
12+18-36=-4 | {5,4} ? |
||||
| {5,5} R4.6 |
12+12-30=-4 | self-dual ? |
A group of order 60 | ? | 6 | |
| {12,3} R4.1′ |
24+6-36=-4 |  |
{3,12} ? |
A group of order 72 |  |
3 |
| {3,12} R4.1 |
6+24-36=-4 | {12,3} ? |
||||
| {6,6} R4.8 |
6+6-18=-4 | self-dual ? |
A group of order 36 | ? | 3 | |
| {6,6} R4.7′ |
6+6-18=-4 | {6,6} ? |
A group of order 36 | ? | ||
| {6,6} R4.7 |
6+6-18=-4 | {6,6} ? |
||||
| {10,4} R4.4′ |
10+4-20=-4 | {4,10} ? |
A group of order 40 | ? | 2 | |
| {4,10} R4.4 |
4+10-20=-4 | {10,4} ? |
||||
| {16,4} R4.5′ |
8+2-16=-4 | {4,16} ? |
A group of order 32 | ? | 1 | |
| {4,16} R4.5 |
2+8-16=-4 | {16,4} ? |
||||
| {12,6} R4.9′ |
4+2-12=-4 | {6,12} ? |
A group of order 24 | ? | 1 | |
| {6,12} R4.9 |
2+4-12=-4 | {12,6} ? |
||||
| {10,10} R4.11 |
2+2-10=-4 | self-dual ? |
A group of order 20 | ? | 1 | |
| {18,9} R4.10′ |
2+1-9=-4 | {9,18} ? |
A group of order 18 | ? | ½ | |
| {9,18} R4.10 |
1+2-9=-4 | {9,18} ? |
||||
| {16,16} R4.12 |
1+1-8=-4 | self-dual ? |
A group of order 16 | ? | ½ |
The things listed below are not regular maps.
| Schläfli symbol | V+F-E=Eu | thumbnail (link) |
|---|---|---|
| {3,9} | 24+8-36=-4 |  |
Index to other pages on regular maps;
indexes to those on
S0
C1
S1
S2
C4
C5
S3
C6
S4.
Some pages on groups
Copyright N.S.Wedd 2009,2010