This page is obsolete. See the current version of Regular Maps in the non-orientable surface of genus 4

Regular Polyhedra on the Genus-C⁴ non-Orientable Manifold

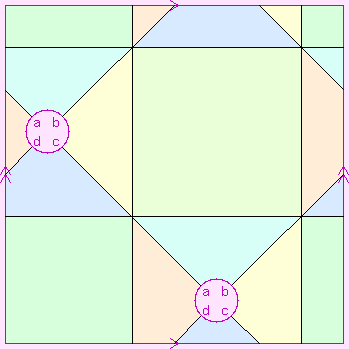
This page shows some of the regular maps that can be drawn on the genus-4c (a sphere plus four crosscaps) non-orientable manifold. For the purpose of these pages, a "regular map" is defined here.

To draw these maps, we need a way of portraying this surface in 2-space. Pink letters show how the "cut edges" are to be joined up, and light pink regions are not part of the surface. This is further explained by the page Representation of 2-manifolds.

Schläfli symbol C&D no.	V+F-E=Eu	thumbnail (link)	dual Petrie dual	Symmetry Group	comments	qy
{6,4}3 N4.2′	6+4-12=-2		next S1{3,6}(2,2)	[48]		2
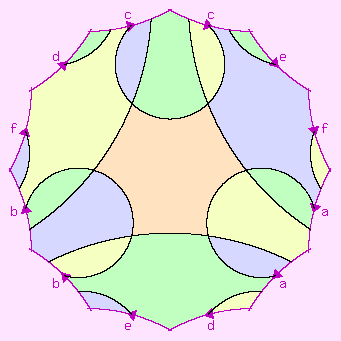
{4,6}3 N4.2	6+4-12=-2		prec. octahedron
{6,4}6 N4.1′	6+4-12=-4		next self	[48]	cantankerous	2
{4,6}6 R4.1	4+6-12=-4		prec.

The things listed below are not regular maps.

{18,3}	6+1-9=-2		{3,18}	D6	∄ See {3,18} for an unconvincing proof.
{3,18}	1+6-9=-2		{18,3} The triangular prism
{8,3}	16+6-24=-2		{3,8}
{3,8}	61+6-24=-2		{8,3}