Regular Maps on the C6 non-Orientable Manifold
This page shows some of the regular maps that can be drawn on the
genus-C6 (a sphere plus six crosscaps) non-orientable
manifold. For the purpose of these pages, a "regular map" is
defined here.
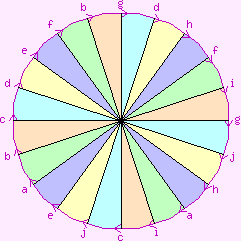
To draw these regular maps, we need a way of portraying this surface in
2-space. We can use the diagram shown to the right: note the regular
but non-obvious arrangement of the labels on the edges of this icosagon,
which seems well-suited for drawing regular polyhedra in theis manifold.
The surface itself is shown in white, the pink letters show how the "cut
edges" are to be joined up, and the light pink regions are not part of
the surface. This is further explained by the page
Representation of 2-manifolds.
Schläfli
symbol
C&N no. | V+F-E=Eu | thumbnail
(link) | dual
Petrie dual | Symmetry
Group | comments | qy |
|---|
{5,4}
N6.3′ |
20+16-40=-4 |
|
{4,5}
? |
A group of order 80 |
? |
8 |
{4,5}
R6.3 |
16+20-40=-4 |
|
{5,4}
? |
{10,3}5
N6.2′ |
20+6-30=-4 |
 |
{3,10}
dodecahedron |
S5 |
 |
3 |
{3,10}5
N6.2 |
6+20-30-4 |
 |
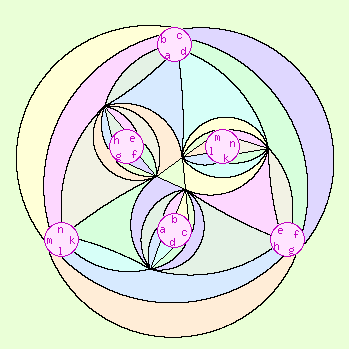{10,3}
S4:{5,10} |
{10,3}10
N6.1′ |
20+6-30=-4 |
 |
{3,10}
|
S5 |
This is the Desargues graph. Its girth is 6.
|
3 |
{3,10}10
N6.1 |
6+20-30-4 |
|
{10,3}
|
The things listed below are not regular maps.
| {6,5} |
6+5-15=-4 |
 |
{6,5} |
|
Irregular
|
2½ |
| {5,6} |
5+6-15-4 |
 |
{5,6} |
| {20,4} |
5+1-10=-4 |
 |
{4,20}
|
D40 |
Irregular  
|
½ |
| {4,20} |
1+5-10=-4 |
 |
{20,4}
|